2021. 7. 12. 17:59ㆍBlockchain
이전 장에서 유한체와 타원곡선이 무엇인지 각각 살펴보았다.
유한체라 함은 여러 조건(덧셈에 닫힘, 항등원, 역원의 존재... 등)을 만족하는 유한개의 원소를 가진 집합이고,
타원 곡선에서는 점 덧셈이라는 것을 하는데, 우리가 익히 알고있는 실수 간의 덧셈의 방식이 아니라 특이하게
수행되는 연산방식을 말한다.
놀랍게도, 실수체 뿐만 아니라 유한체 위에서 타원곡선이 정의될 수 있다.
다시말해 유한체끼리의 점덧셈이 가능하다는 의미이다.
유한체와 타원곡선
유한체 위에서 정의된 타원곡선은 조금 특이하게 생겼다.
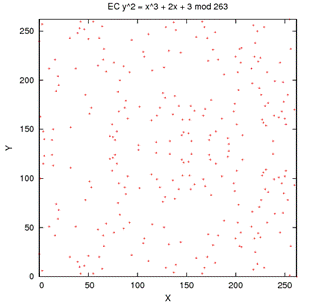
출처 : https://cse.unl.edu/~ssamal/crypto/EEECC.php
'곡선'이라는 말이 무색하게도 점들이 여러군데 산재해있음을 확인할 수 있다.
하지만 이러한 유한체의 타원곡선의 특성 덕분에 secp256k1 암호화가 가능한 것이다.
위 그래프를 자세히 들여다보면, y축의 100과 150 사이쯤의 축을 기준으로 점들이 대칭을 이루고 있음을 알 수 있다.
실제로 위수(나머지 연산에서 나누는 수)가 y값인 축을 기준으로 유한체 타원곡선을 대칭을 이루는데
이는 타원곡선에서 y^2 이기 때문이며, 유한체의 타원곡선에서는 음수가 존재하지 않는다.
또한 유한체에서의 타원곡선 역시 우리가 이전 장에서 본 교환법칙, 결합법칙이 성립한다.
지금부터 유한체에서의 타원곡선을 코드로 구현해보도록 하겠다.
from ecc.FieldElement import FieldElement
from ecc.Point import Point
P = 2 ** 256 - 2 ** 32 - 977
class S256Field(FieldElement):
def __init__(self, num, prime=None):
super().__init__(num, prime=P)
def __repr__(self):
return '{:x}'.format(self.num).zfill(64)
def sqrt(self):
return self ** ((P + 1) // 4)secp256k1만의 타원곡선을 정의하기 위해 특별한 FieldElement를 정의한다.
S256Field 클래스는 FieldElement를 상속한다.
secp256k1에서의 P를 정의해주었으며, prime(위수)을 따로 받지않고 위에서 따로 정의된 P를 prime에 넣어준다.
또한 유한체의 원소이기 때문에 제곱근을 구하는 함수 sqrt 역시 위와 같은 연산이 가능하다.
from ecc.Point import Point
from ecc.S256Field import S256Field
A = 0
B = 7
N = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
P = 2**256 - 2 ** 32 - 977
class S256Point(Point):
def __init__(self, x, y, a = None, b = None):
a = S256Field(A)
b = S256Field(B)
if type(x) == int:
x = S256Field(x)
y = S256Field(y)
super().__init__(x, y, a, b)
else:
super().__init__(x, y, a, b)
def __repr__(self):
if self.x is None:
return 'S256Point(infinity)'
else:
return 'S256Point({}, {})'.format(self.x, self.y)secp256k1의 매개변수 A, B를 지정해주었고, 생성점 G에 스칼라곱하였을 때 처음으로 무한원점에 도달하게끔 하는 수,
다시말해 생성점으로 하여금 유한군(finite group)을 구성하도록 하는 수인 N을 정의한다.
생성점 G에 대해, 스칼라 곱을 반복해서 한다면 특정값 N에서 N*G가 무한원점에 도달한다.
처음 무한원점에 도달하기까지의 스칼라곱들을 집합으로 구성하면 {G, 1*G, 2*G, . . . , N*G}가 되고
이를 유한군(finite group)이라고 한다.
y^2 = x^3 + 7 의 식을 만족하도록 A, B를 정의하여 S256Field 객체를 생성한다. 만일 x가 int 형태로 들어왔다면
이 역시 S256Field 객체로 만들고, 이 파라미터들을 모아서 S256Point를 만든다.
from ecc.S256Point import S256Point
from keys.Signature import Signature
from random import randint
G = S256Point(0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798,0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
N = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
class PrivateKey:
def __init__(self, secret):
self.secret = secret
self.point = secret * G
def hex(self):
return '{:x}'.format(self.secret).zfill(64)
def sign(self, z):
k = randint(0, N)
r = (k * G).x.num
k_inv = pow(k, N-2, N)
s = (z + r*self.secret) * k_inv % N
if s > N/2:
s = N - s
return Signature(r, s)비밀키 클래스인 PrivateKey이다. 생성자에서 비밀키인 e를 인자로 받고
생성점 G를 정의하고, 이를 비밀키와 스칼라 곱하여 공개키인 point를 멤버변수로 저장한다.
서명을 생성하는 sign 함수는 서명 생성 절차에 따라 서명을 생성하고 이를 담는 Signature 객체를 반환한다.
class Signature:
def __init__(self, r, s):
self.r = r
self.s = s
def __repr__(self):
return 'Signature({:x},{:x})'.format(self.r, self.s)마지막으로 서명값인 r, s를 담는 Signature 클래스이다.
from ecc.S256Point import S256Point
G = S256Point(0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798,
0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
A = 0
B = 7
N = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
P = 2**256 - 2 ** 32 - 977
class Verify:
def sig_verify(self, sig, z, pubkey):
s_inv = pow(sig.s, N - 2, N)
u = z * s_inv % N
v = sig.r * s_inv % N
total = u * G + v * pubkey
print('calculated r : ', hex(total.x.num))
return total.x.num == sig.r서명을 검증하는 Verify 클래스에서는 서명 객체(Signature), (해시된)메시지 z, 공개키를 인자로 받아 검증을 수행한다.
위의 절차를 통해 계산된 total의 x값이 서명의 r값과 동일하면 올바르게 서명된 것으로 간주한다.
지금까지 구현된 코드를 통해 서명을 검증할 수 있는지 확인해보자.
e = int.from_bytes(hash256(b"Project_Shawshank"), 'big')
z = int.from_bytes(hash256(b'Latte_is_a_horse.'), 'big')
pv_key = PrivateKey(e)
pubkey = pv_key.point
sig = pv_key.sign(z)
print('message z : ', z)
print('private key : ', pv_key)
print('public key : ', pubkey)
print('signature : ', sig)
verf = Verify()
print(verf.sig_verify(sig, z, pubkey))
결과값>>>
message z : 85790332922056139876445043133174718613728128661300119318805742491686086099563
private key : <keys.PrivateKey.PrivateKey object at 0x000001ECA8CFC820>
public key : S256Point(9b8ad550a2aa8fb93b97a7aee477522f49505c63d9d8c6cca3b32c81dcfe01e3, 1236777e478e579ac69e4c25d2ec691cddee5ab1d0b1b5381be20ff2f20361d4)
signature : Signature(e711a78046ed19ea83ebc30a28bb20042441023ed679092598f8d7fb064f0f29,47c7441a963670cce7186e8c6693fd6476b0f63917fe5c9bde68cbbfda416651)
calculated r : 0xe711a78046ed19ea83ebc30a28bb20042441023ed679092598f8d7fb064f0f29
TrueVerify 클래스의 sig_verify 메서드로 계산된 r값이 서명 Signature 객체의 x값과 동일한 것을 확인할 수 있다.
sig_verify 함수는 True를 반환한다.
'Blockchain' 카테고리의 다른 글
| [밑바닥비트코인] 6. 트랜잭션(Transaction) (1) | 2021.07.20 |
|---|---|
| [밑바닥비트코인] 5. 직렬화 (2) | 2021.07.15 |
| [밑바닥비트코인] 3. 타원곡선 (2) | 2021.07.04 |
| [밑바닥비트코인] 2. 유한체의 연산 (0) | 2021.07.04 |
| [밑바닥비트코인] 1. 유한체(Finite field) (0) | 2021.07.04 |