2021. 10. 1. 00:13ㆍDeep Learning
본 게시글은 한빛미디어 『밑바닥부터 시작하는 딥러닝, 사이토 고키, 2020』의 내용을 참조하였음을 밝힙니다.
기계학습에서 학습이 이루어지는 근간이자 수단이 바로 '미분'이다.
이 미분이란 무엇이고, 기계 학습에서 어떻게 이용될까?
수치 미분 / 편미분
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value)
출처 : https://en.wikipedia.org/wiki/Derivative
위키디피아에 따르면 미분은 어떠한 함수에 대해서 argument(인수)의 변화에 대해서 함수 값이 변하는 민감도를
측정한다. 다시 말하자면 미분이란 함수에서 특정 변수가 변할 때, 함수값이 변하는 정도를 측정하는 방법이다.
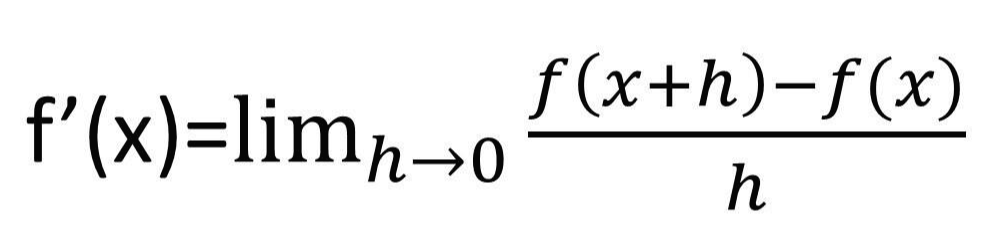
위를 코드로 구현해보자.
h = 1e-4
def numerical_diff(f, x):
return (f(x+h)-f(x-h))/(2*h)함수 f의 특정 x값에서의 미분값을 계산하였다. 정확한 미분 공식에 따라 계산하려면 어느 정도 오차가 생길 수밖에
없기 때문에 x값 전후로 아주 작은 값인 h을 더해/빼서 이의 기울기를 계산한다. 위와 같은 방식을
중앙 차분이라고 한다.
>>> def f(x):
return x**2 + 3*x + 5
>>> numerical_diff(f, 2)
7.000000000019213
다음으로 편미분(partial derivative)이 무엇인지 알아보자.
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary).
출처 : https://en.wikipedia.org/wiki/Partial_derivative
다변수 함수에서 편미분이란 (다른 변수들은 상수로 고정시킨 뒤) 한 변수에 대해서 미분하는 것을 말한다.
함수에 (예를 들면) x 이외에도 y, z 등 여러 변수들이 있을 수 있는데, 이 중에서 x에 대해서만 미분하고 싶다면
y, z 등 다른 변수들은 고정한 채 x만을 변화시켰을 때 함수값이 얼마나 변하는지를 측정한 값(혹은 방정식)이다.

출처 : https://towardsdatascience.com/step-by-step-the-math-behind-neural-networks-d002440227fb
위와 같이 모든 변수 각각에 대해 편미분하여 벡터로 정리한 것을 gradient라고 한다.
def numerical_gradient(f, x):
grad = np.zeros_like(x)
for i in range(x.size):
tmp_val = x[i] #x[i]의 원래값을 저장해둔다.
x[i] = tmp_val + h
fxh1 = f(x) #x[i]가 약간 증가한 형태일 때의 f값을 계산
x[i] = tmp_val - h
fxh2 = f(x) #x[i]가 약간 감소한 형태일 때의 f값을 계산
grad[i] = (fxh1-fxh2)/(2*h) #x[i]만 바뀌었을 때의 기울기 계산
x[i] = tmp_val
return grad변수들의 리스트인 x와 동일한 형태(shape)의 넘파이 배열인 grad를 만든다.
x에 있는 변수들을 순회하면서 변수(x[0], x[1], x[2]..)마다 그에 대한 미분값을 구해서 이를 i번째 grad에 저장한다.
>>> def f(x):
return x[0]**2 + 5*x[1] + 2*x[2]**2
>>> x = np.array([3.0, 2.0, 1.0])
>>> numerical_gradient(f, x)
array([6., 5., 4.])위 코드는 함수 f에 대해 x[0] = 3.0, x[1] = 2.0, x[2] = 1.0일 때의 gradient 값을 구한 것이다.
'Deep Learning' 카테고리의 다른 글
| [밑바닥딥러닝] 8. 2층 신경망 구현, 미니배치 학습 (0) | 2021.10.01 |
|---|---|
| [밑바닥딥러닝] 7. 경사하강법(gradient descent) (0) | 2021.10.01 |
| [밑바닥딥러닝] 5. 신경망 학습 - 손실 함수, 미니 배치 학습 (0) | 2021.09.30 |
| [밑바닥딥러닝] 4. 신경망 구현 - 손글씨 인식 (1) | 2021.09.12 |
| [밑바닥딥러닝] 3. 신경망 구현, 소프트맥스(softmax) (0) | 2021.09.12 |