2021. 5. 4. 13:29ㆍMachine Learning
서포트 벡터 머신(SVM)은 선형, 비선형 분류, 회귀, 이상치 탐치 등 범용적으로 쓰일 수 있는 머신러닝 모델이다.
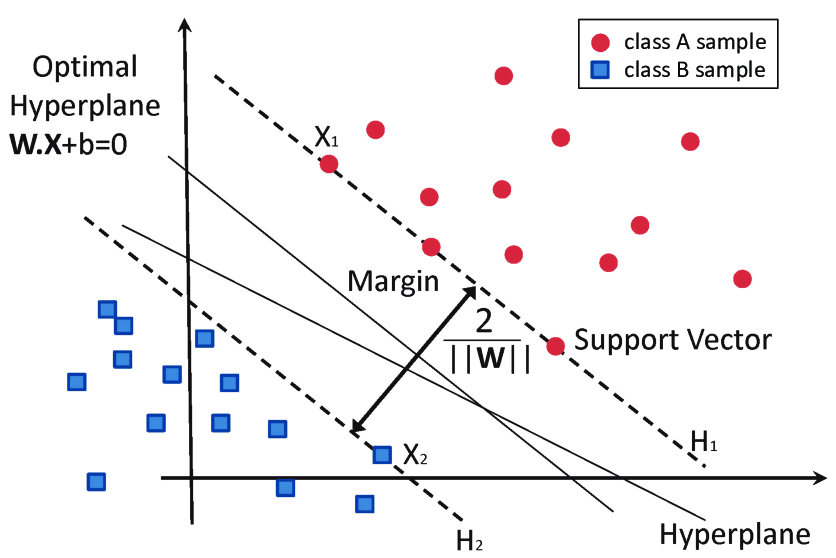
출처 : www.researchgate.net/figure/SVM-6-Shows-the-main-concept-of-SVM-Its-margins-and-support-vectors_fig1_343997587
서포트 벡터 머신은 위 그림과 같이 데이터를 클래스로 분류할 때 클래스 간의 가장 넓은 거리(Margin)를 찾는 모델이다.
그래서 라지 마진 분류(Large Margin Classification)라고도 한다.
마진의 끝자락에 위치한 샘플에 의해 마진이 결정되는데, 이러한 샘플을 서포트 벡터라고 한다.
소프트 마진 분류
모든 샘플이 마진의 바깥쪽에 완벽하게 분류되어있다면 이를 하드 마진 분류라고한다.
하지만 하드 마진 분류 방식은 이상치에 민감하며, 선형적 데이터에 특히 적합하다는 한계점을 지니고 있어
마진 오류(샘플이 마진 중간에 있거나 반대편에 있는 경우)를 허용하지 않는다면 모델의 일반화에도 좋지 않을 것이다.

출처 : noviceprogramming667661022.wordpress.com/author/kewlwasabi/
이 한계를 극복하기 위해 만들어진 것이 소프트 마진 분류인데, 마진 오류를 어느정도 허용하여 마진을 최대한 넓게
가져가고자한 모델이다. 사이킷런의 SVM 모델에서 하이퍼파라미터 C를 통해 이를 조절할 수 있다.
선형 SVM 분류 실습
4장에서 실습한 Iris 데이터셋을 통해 서포트 벡터 머신을 훈련시켜보겠다.
iris = datasets.load_iris()
X = iris["data"][:, (2,3)] #length, width
y = (iris["target"]==2).astype(np.float64) #Iris-Virginica 1 or 0
svm_clf = Pipeline([("scaler", StandardScaler()),
("linear_svc", LinearSVC(C=1, loss="hinge"))])
svm_clf.fit(X,y)표준화 변환기와 SVM 모델을 파이프라인으로 연결한 뒤, SVM을 훈련시켰다.
for x_i in X:
result = svm_clf.predict([[x_i[0], x_i[1]]])
if result==1:
plt.scatter(x_i[0], x_i[1], c='red')
else:
plt.scatter(x_i[0], x_i[1], c='blue')
plt.xlabel("width")
plt.ylabel("length")
plt.grid()
plt.show()SVM 모델이 각 샘플을 Iris-Virginica로 분류할 경우 scatter 그래프에 붉은 색으로,
이 외의 클래스로 분류할 경우 파란 색으로 표시하도록 하였다.
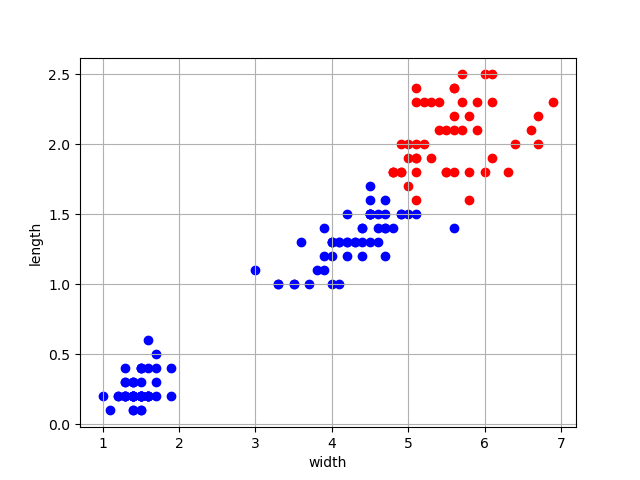

4장의 분류기법을 사용했다면 2개의 하이퍼플레인(Hyperplane)을 통해 이 데이터셋을 분류했을테지만
서포트 벡터 머신을 통해 간단하게 Large Margin을 찾는 것으로 클래스 분류가 이루어졌다.
4장에서 살펴봤듯이 width(꽃잎의 너비)가 1.6 부근에서 클래스 분류가 이뤄졌고, length(길이) 정보도
선형 분류에 따르면 5 부근에서 클래스 분류가 이뤄졌다. 따라서 SVM 모델은 올바르게 데이터셋을 분류했다.
'Machine Learning' 카테고리의 다른 글
| 6. 결정 트리(Decision Tree) (0) | 2021.05.04 |
|---|---|
| 5-2. 서포트 벡터 머신(SVM) - 비선형 SVM 분류 (0) | 2021.05.04 |
| 4-2. 소프트맥스 회귀(Softmax Regression) (1) | 2021.05.02 |
| 4-1. 로지스틱 회귀(Logistic Regression) (0) | 2021.05.02 |
| 3-2. 규제 - 라쏘 회귀, 엘라스틱 넷 (1) | 2021.04.27 |