2021. 5. 2. 20:55ㆍMachine Learning
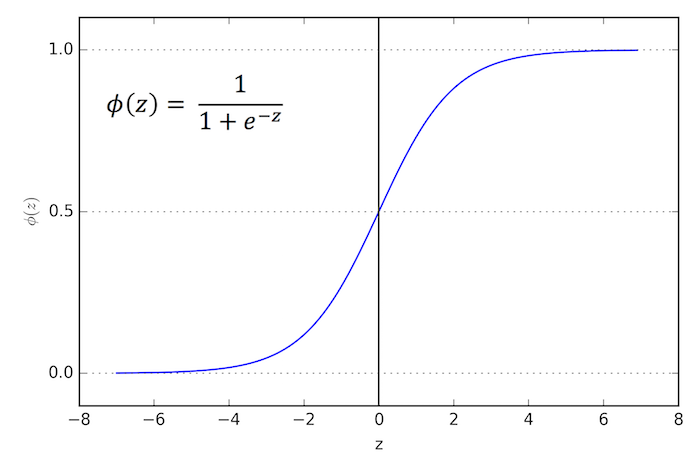
시그모이드 함수

출처: medium.com/@msdasila90/logistic-regression-and-its-mathematical-implementation-13f96ee71c8c
로지스틱 회귀는 어떤 입력값 X에 대해 양성 클래스(1)와 음성 클래스(0)으로 구분하는 분류 방법이다.
이를 '이진 분류기'라고 한다.
출처 : laptrinhx.com/machine-learning-using-c-a-beginner-s-guide-to-linear-and-logistic-regression-2294098464/
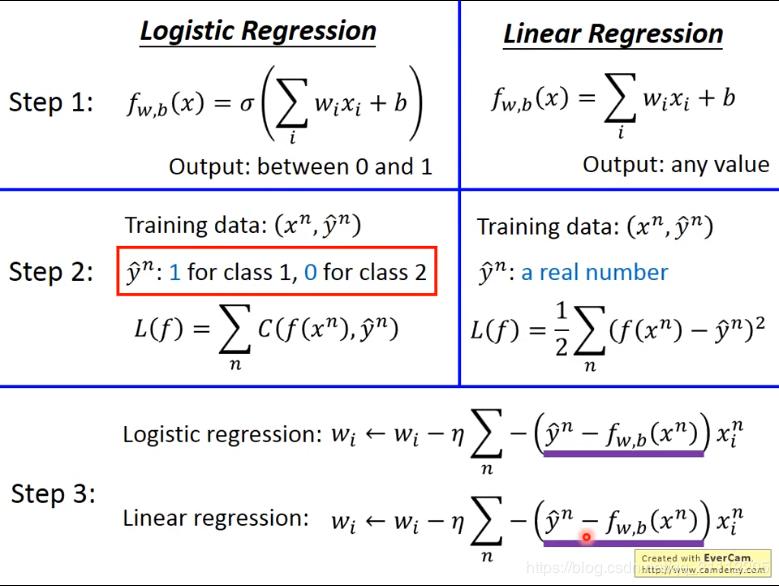
로지스틱 회귀 모델에서는 가중치와 input(x0, x1, x2, .... xn)을 곱한 값을 시그모사이드 함수에 통과시키는데,
이 값(hθ(x))이 0.5보다 클 경우, 양성 클래스(1), 0.5보다 작을 경우 음성 클래스(0)로 분류한다.
출처 : www.programmersought.com/article/21582256379/
시그모이드 함수의 x축의 값(가중치와 특성값의 곱)을 로짓이라고 하는데, 로짓 값이 0보다 클 경우 양성 클래스가 되고,
0보다 작을 경우 음성 클래스가 된다.
로지스틱 회귀의 업데이트

출처 : towardsdatascience.com/optimization-loss-function-under-the-hood-part-ii-d20a239cde11
로지스틱 회귀의 업데이트 역시 마찬가지로 비용함수에 의해 이뤄진다.
출처 : medium.com/analytics-vidhya/derivative-of-log-loss-function-for-logistic-regression-9b832f025c2d
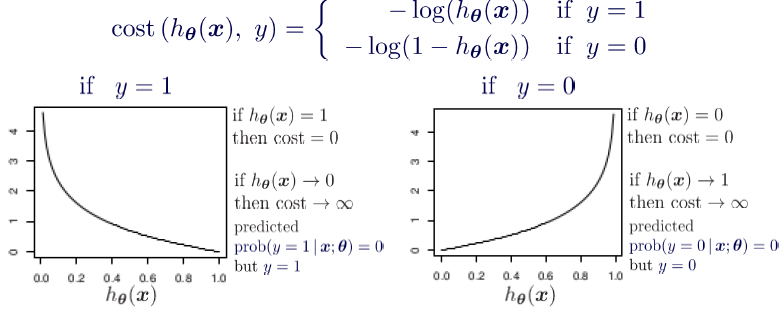
위 비용함수에서
y값은 hθ(x)이 0.5 이상일 경우 1이고, 0.5 이하일 경우 0이다.
hθ(x) 값이 0.5보다 크다면(양성이라면) log(hθ(x))은 0에 가까울 것이고, log(1-hθ(x))은 -∞에 가까울 것이다.
→ 예측값 y == 1일 경우 비용함수가 0에 수렴
hθ(x) 값이 0.5보다 작다면(음성이라면), log(hθ(x)) -∞에 가까울 것이다. log(1-hθ(x))은 0에 가까울 것이다.
→ 예측값 y==1일 경우 비용함수가 매우 커진다(∞)
해당 계산을 모든 샘플수(m)에 대해서 평균을 낸 것이 로지스틱 회귀의 비용함수이다.
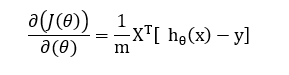
위 식은 로지스틱 비용함수를 가중치에 대해서 미분한 식이다. 예측값(hθ(x))과 타깃값(y)의 오차를 계산하고,
(미분한 가중치와 매칭되는)특성값을 곱하여 모든 샘플에 대해 평균을 계산한다.
실습
iris = datasets.load_iris()
print(list(iris.keys()))
X = iris["data"][:, 3:] #iris 데이터의 마지막 열(너비)만 추출
y = (iris["target"]==2).astype(np.int) #Iris-Virginica 1 or 0
log_reg = LogisticRegression()
log_reg.fit(X,y)붓꽃 데이터셋을 통해 로지스틱 회귀를 실습한다.
입력값(특성값)으로 iris 데이터셋의 너비 정보를 추출하여 X 열 벡터에 저장하고
양성/음성 클래스 분류를 위해 iris의 target 값이 2일 경우(Iris-Virginica)를 1과 0으로 나누어 y값에 저장하였다.
LogisticRegression 클래스를 호출하여 로지스틱 모델을 훈련시켰다.
X_new = np.linspace(0,3,1000).reshape(-1,1)
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:,1], "g-")
plt.plot(X_new, y_proba[:,0], "b--")
plt.xlabel('width')
plt.ylabel('probability')
plt.legend(['Iris virginica','Not Iris virginica'])
plt.grid()
plt.show()예측 모델이 어떠한 양상으로 예측하였는지 확인하기 위해 0~3까지의 연속적인 1000개의 수를 생성하여
이 수를 훈련시킨 모델에 input으로 넣고 그에 대한 출력을 y에 저장하였다.
로지스틱 회귀의 predict_proba 메서드는 주어진 X_new 값에 대해서 0과 1로 예측한 확률을 반환한다.
[[9.99250016e-01 7.49984089e-04]
[9.99240201e-01 7.59799387e-04]
[9.99230257e-01 7.69743043e-04]
...
[3.08374822e-03 9.96916252e-01]
[3.04400296e-03 9.96955997e-01]
[3.00476842e-03 9.96995232e-01]]
width 값이 1.6 근처에서 양성 클래스와 음성 클래스가 역전된다.
예측 모델이 이 수치 부근에서 올바르게 예측을 할 수 없음을 의미할 수 있다. 이 수치를 결정 경계라고 한다.
'Machine Learning' 카테고리의 다른 글
| 5-1. 서포트 벡터 머신(SVM) - 선형 SVM 분류 (1) | 2021.05.04 |
|---|---|
| 4-2. 소프트맥스 회귀(Softmax Regression) (1) | 2021.05.02 |
| 3-2. 규제 - 라쏘 회귀, 엘라스틱 넷 (1) | 2021.04.27 |
| 3-1. 규제 - 릿지 회귀(Ridge Regression) (0) | 2021.04.27 |
| 2-2. 학습 곡선(Learning Curve) (1) | 2021.04.27 |