2021. 4. 27. 21:36ㆍMachine Learning
이전 장에서 살펴봤듯이, 예측 모델이 훈련세트에만 정확하게 예측하도록 훈련되어 검증 세트에서의 효과가
떨어지는 것을 과대 적합이라고 한다. 이러한 과대 적합 문제를 해결하는 방법 중 하나가 '규제'이다.
선형 회귀 모델에서는 가중치에 제한을 둠으로써 규제를 가한다.
이러한 규제의 종류로는 크게 '릿지' 회귀, '라쏘' 회귀, 엘라스틱넷이 있다.
릿지 회귀(Ridge regression)
릿지 회귀는 기존 선형 모델에 규제항을 추가한 회귀 모델이다.
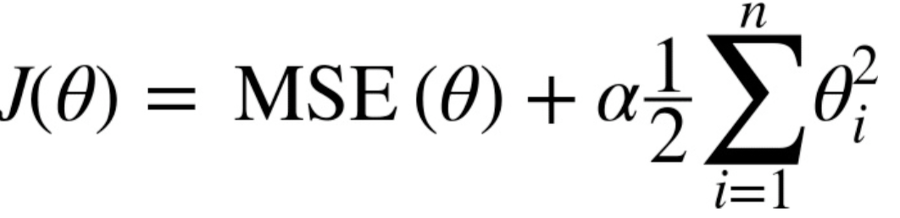
릿지 회귀의 비용함수는 기존 MSE 비용함수에서 가중치 벡터 w 의 L2 norm이 추가된다.
각 가중치의 제곱을 모두 합한 후, 규제의 강도를 결정하는 하이퍼 파라미터 alpha를 추가한다.
1/2는 미분 시 편의를 위한 상수이다. 이 때 첫번째 파라미터(즉, 편향(bias))는 계산의 대상이 되지 않는다.
모델을 훈련시킬 수록 비용함수가 작아지는 방향으로 진행되는데, 이에 따라 가중치가 과도하게 커지는 것을
방지할 수 있다.
이전 장의 예제를 활용하여 릿지 회귀를 적용해보자.
m = 20
X = 20*np.random.rand(m,1) - 10
y = 0.5*X**2 + X + 2 + np.random.rand(m,1)*100y값의 randomness를 증가시키기 위해 랜덤수 생성기에 100을 곱하였다.

polynomial_reg = Pipeline([
("poly_feathers", PolynomialFeatures(degree=10, include_bias=False)),
("ridge_reg", Ridge(alpha=0.5, solver="cholesky")),
])그 다음 10차 다항 특성을 추가하는 변환기와 릿지 회귀를 파이프 라인으로 연결한다.
릿지 회귀의 alpha 값을 변경하면 어떤 변화가 생기는지 비교해볼 것이다.
X_test = 10*np.random.rand(100,1) - 5
polynomial_reg.fit(X, y)
y_test_pred = polynomial_reg.predict(X_test)규제의 영향을 알아보기 위하여 테스트 셋을 생성하고, 생성한 파이프라인을 통해 변환하고, 모델을 훈련시켰다.

위 그래프는 alpha값을 0, 0.3, 1로 변경함에 따라 예측 모델이 계산한 예측값을 나타낸다.
규제의 alpha값을 증가시킬수록 그래프가 더 평평해지는데, 이는 훈련 데이터에 과대적합이 될 확률이 줄어든다는 것을
의미한다.
'Machine Learning' 카테고리의 다른 글
| 4-1. 로지스틱 회귀(Logistic Regression) (0) | 2021.05.02 |
|---|---|
| 3-2. 규제 - 라쏘 회귀, 엘라스틱 넷 (1) | 2021.04.27 |
| 2-2. 학습 곡선(Learning Curve) (1) | 2021.04.27 |
| 2-1. 다항 회귀(Polynomial Regression) (0) | 2021.04.26 |
| 1-3. 경사 하강법(Gradient descent) - 확률적 경사 하강법(SGD), 미니배치 경사 하강법 (1) | 2021.04.26 |