2021. 4. 27. 18:59ㆍMachine Learning
분석하고자 하는 대상을 모델을 통해 분석할 경우, 올바르게 훈련시켰는지 아닌지 판단이 안 설 수 있다.
훈련 세트에만 과도하게 정확한 예측 모델을 만들었을 경우를 '과대 적합'이라하고,
과대 적합을 피하려하다보니 모델이 약하게 훈련될 경우를 '과소 적합'이라고 한다.
예측 모델이 과대 적합되었을 경우 일반화가 잘 이루어지지 않아서 테스트 세트에서는 예측이 안 맞을 수도 있고,
과소 적합되었을 경우, 정확한 예측 모델이라고 하기 힘들다.
과대 적합, 과소 적합을 판단하기 위한 몇 가지 방법이 존재하는데, 이 중 하나가 학습 곡선(Learning Curve)이다.
학습 곡선은 예측 모델을 통해 만들어진 훈련 세트와 검증 세트의 모델 성능 간의 차이를 나타내는 그래프이다.
X축은 반복(iteration)으로, Y축은 비용 함수 값(모델이 만든 Cost)로 나타낸다.
def plot_learning_curves(model, x, y):
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)
train_err = []
val_err = []
for m in range(1, len(X_train)):
model.fit(X_train[:m], y_train[:m])
y_train_pred = model.predict(X_train[:m])
y_val_pred = model.predict(X_val)
cost_train = mean_squared_error(y_train_pred, y_train[:m])
cost_val = mean_squared_error(y_val_pred, y_val)
train_err.append(cost_train)
val_err.append(cost_val)
plt.plot(np.sqrt(train_err),"r-+")
plt.plot(np.sqrt(val_err), "b-")
plt.legend(['Train error', 'Val Error'])
plt.grid()
plt.show()먼저 파라미터로 받은 모델을 훈련 세트로 훈련시키는데, for문을 통해 훈련 세트의 크기를 하나씩 늘려나간다.
그 다음 예측 모델을 통해 예측한 훈련 데이터의 예측값과 타깃값의 비용을 계산하고,
검증 데이터의 예측값과 타깃값 간의 비용을 계산하여 준비한 배열에 각각 넣어준다.
polynomial_reg1 = Pipeline([
("poly_feathers", PolynomialFeatures(degree=2, include_bias=False)),
("lin_reg", LinearRegression()),
])
plot_learning_curves(polynomial_reg1,X,y)먼저 2차항의 특성만을 추가한 데이터를 선형 회귀로 분석해보자.
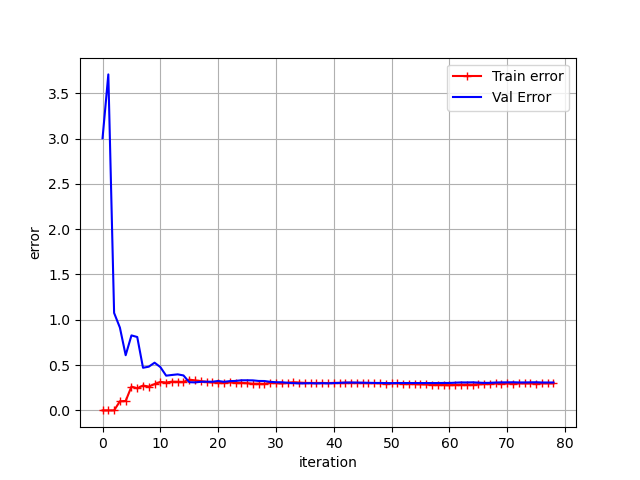
가장 먼저 m=1이었을 때, 예측 모델은 하나의 데이터만을 학습했기 때문에 훈련 세트에서는 오차가 0이지만,
검증 세트에서는 매우 큰 오차를 보인다. m이 커짐에 따라(훈련시킬 데이터의 수를 늘려감에 따라)
훈련 데이터에서의 오차가 증가하면서 훈련 세트와 검증 세트의 비용 간 차이가 작아진다.
polynomial_reg2 = Pipeline([
("poly_feathers", PolynomialFeatures(degree=10, include_bias=False)),
("lin_reg", LinearRegression()),
])
plot_learning_curves(polynomial_reg2,X,y)먼저 10차항의 특성을 추가한 데이터를 선형 회귀로 분석하여 비교해보자.
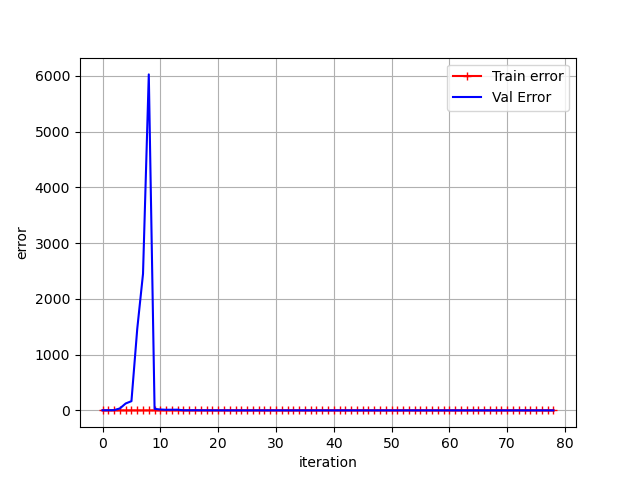
훈련 세트에서의 예측에서의 타깃값과의 오차는 거의 0에 수렴하지만, 훈련 세트 크기가 크지 않은 경우( x<10)에서의
검증 세트 오차는 매우 크다. 하지만 훈련 세트가 커짐에 따라 검증 세트 오차 역시 줄어드는 양상을 보인다.
무슨 일이 일어나는지 y축의 범위를 0 ~ 0.5로 제한하여 확대해 살펴보자.


확실히 10차항의 학습곡선에서의 훈련세트 오차와 검증세트 오차간의 차이가 2차항 학습곡선에서의 그것보다
더 넓다는 것을 확인할 수 있다. 이렇게 검증 세트에서의 오차가 더 크다는 것은 예측 모델이 과대적합되었다는 사실을
나타낸다.

출처 : Hands-On Machine Learning with Scikit-Learn, Keras & Tensorflow 2판, Aurélien Géron
위의 예시처럼 다항특성을 과도하게 추가할 경우, 훈련 세트에는 정확한 예측 모델을 만들어낼 수 있지만, 검증 세트에서
는 효과가 약할 수 있다. 다음 장에서 이러한 과대적합 현상을 방지할 수 있는 기법에 대해 알아본다.
'Machine Learning' 카테고리의 다른 글
| 3-2. 규제 - 라쏘 회귀, 엘라스틱 넷 (1) | 2021.04.27 |
|---|---|
| 3-1. 규제 - 릿지 회귀(Ridge Regression) (0) | 2021.04.27 |
| 2-1. 다항 회귀(Polynomial Regression) (0) | 2021.04.26 |
| 1-3. 경사 하강법(Gradient descent) - 확률적 경사 하강법(SGD), 미니배치 경사 하강법 (1) | 2021.04.26 |
| 1-2. 경사 하강법(Gradient Descent) - 배치 경사 하강법 (0) | 2021.04.26 |