2021. 4. 26. 20:55ㆍMachine Learning
확률적 경사 하강법(SGD)
경사 하강법의 두번째 방법은 확률적 경사 하강법(SGD)이다.
배치 경사 하강법의 단점은, 추정한 파라미터를 전체 샘플에 적용하고,
그에 대한 비용함수와 그레디언트를 계산할 때도 전제 샘플을 사용한다는 것이다.
이는 훈련 샘플 크기가 매우 커질 경우, 시간적 비용이 크게 들게 된다.
확률정 경사 하강법(SGD)는 파라미터를 업데이트 매 스텝마다, 하나의 샘플을 무작위로 선택하여
그 하나의 샘플에 대한 비용함수 그레디언트를 계산하고, 파라미터를 업데이트한다.
def SGD_gradient_cost_fun(x_b, y, y_hat):
random_idx = np.random.randint(len(x_b))
x_i = x_b[random_idx:random_idx+1]
y_i = y[random_idx:random_idx+1]
y_hat_i = y_hat[random_idx:random_idx+1]
diff = y_hat_i - y_i
gradient_cost = x_i.T.dot(diff)*2
return gradient_cost
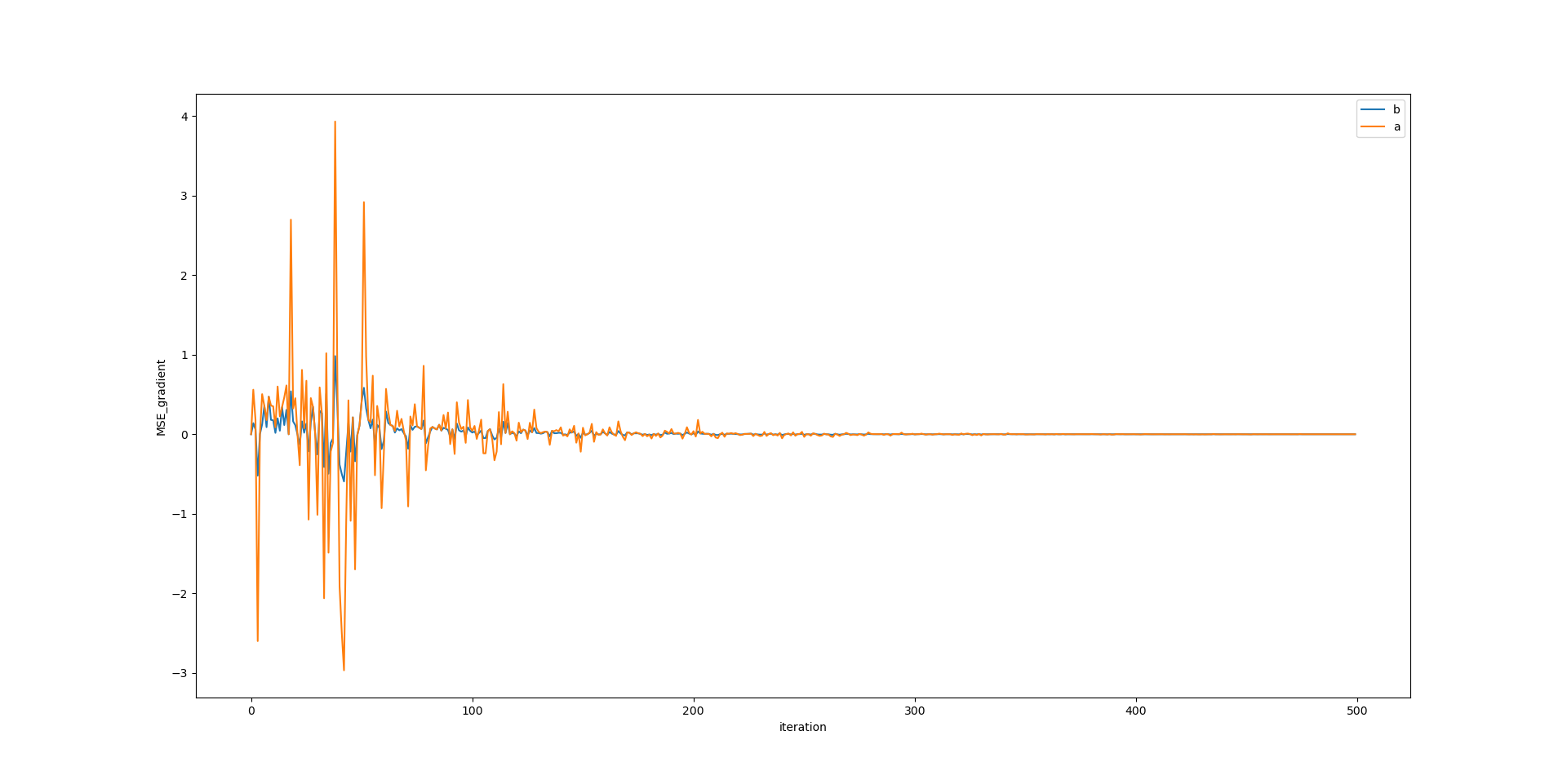
물론 단점도 존재한다. 1-2장에서 살펴본 동일한 예제에 배치 경사 하강법이 아닌,
확률적 경사 하강법을 적용한 코드이다. 샘플을 무작위로 선택하고, 하나의 샘플로 파라미터를 결정하기 때문에
이전 샘플로부터 도출된 파라미터가 다음 샘플에서는 터무니없이 틀린 파라미터일 수 있다.
출처 : www.google.com/url?sa=i&url=https%3A%2F%2Fd2l.ai%2Fchapter_optimization%2Foptimization-intro.html&psig=AOvVaw1B_wI-I77IoSSI3UrNpkL6&ust=1620843685842000&source=images&cd=vfe&ved=0CAIQjRxqGAoTCKii9rKfwvACFQAAAAAdAAAAABCAAQ
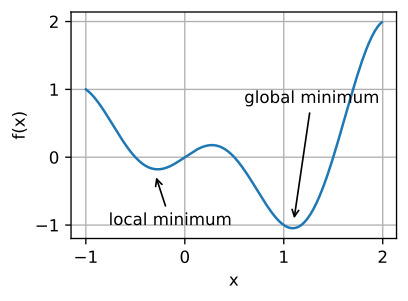
하지만 샘플 선택의 무작위성으로 인해 배치 경사 하강법에 비해 전역 최솟값에 더 가까이 갈 확률이 높다는 장점을
지니고 있다. 하지만 배치 경사 하강법이 전역 최소값에 가까이 진입할 경우,
훨씬 더 정확한 파라미터를 도출할 수 있다. SGD에서는 에포크가 진행할 수록 학습률을 점진적으로 감소시켜나가는
방법을 통해 이러한 단점을 상쇄한다.
미니배치 경사 하강법
미니 배치 경사하강법은 파라미터 업데이트에 전체 샘플을 사용하는 배치 경사 하강법을 경량화한 버전이라고 할 수 있다.
각 업데이트 스텝마다, 전체 샘플에서 일부 샘플 세트를 추출한 뒤, 배치 경사 하강법을 똑같이 적용하는 방법이다.
파라미터 업데이트가 SGD보다 덜 불규칙하게 이뤄지면서, 배치 경사 하강법보다 빠른 계산 속도를 보인다.
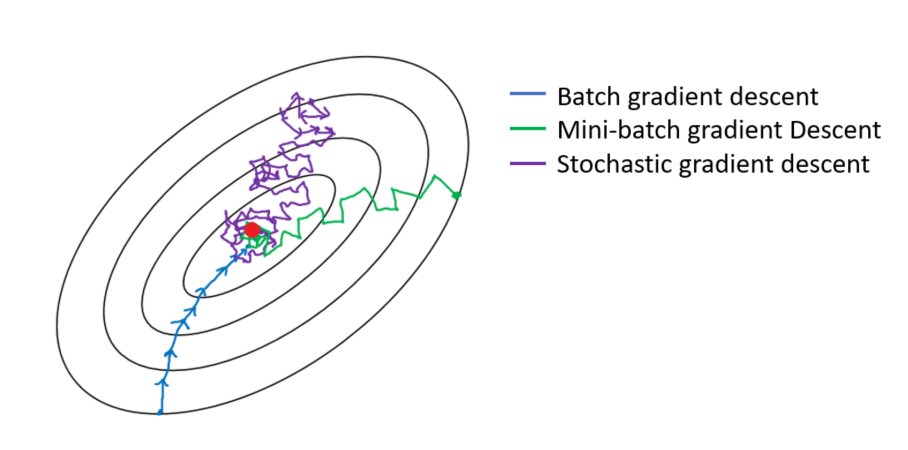
출처 : medium.com/analytics-vidhya/gradient-descent-vs-stochastic-gd-vs-mini-batch-sgd-fbd3a2cb4ba4
'Machine Learning' 카테고리의 다른 글
| 3-1. 규제 - 릿지 회귀(Ridge Regression) (0) | 2021.04.27 |
|---|---|
| 2-2. 학습 곡선(Learning Curve) (1) | 2021.04.27 |
| 2-1. 다항 회귀(Polynomial Regression) (0) | 2021.04.26 |
| 1-2. 경사 하강법(Gradient Descent) - 배치 경사 하강법 (0) | 2021.04.26 |
| 1-1. 선형 회귀(Linear regression) (0) | 2021.04.26 |