2021. 4. 26. 17:03ㆍMachine Learning
우리는 일상 속에서 '선형 모델'을 쉽게 찾아볼 수 있다.
나이에 따른 성인병 발병확률이나, 소득과 비만율과의 상관지수 등이 그 예가 될 수 있다.
선형 회귀(Linear regression)는 이러한 선형 모델을 분석하기 위한 방법으로,
여러 샘플 입력(X)와 그에 대한 결과값(y)가 주어졌을 때
이 데이터셋(dataset)을 분석하여 해당 데이터가 어떤 양상을 띠는지 선(line)으로서 추정하는 모델이다.
X = 2*np.random.randn(50,1)
y = 4 + 3*X + np.random.randn(50,1)
plt.scatter(X,y)
plt.xlabel('X')
plt.ylabel('y')
plt.show()
1의 mean 값을 가지는 50개의 Gaussian Distribution 난수를 X와 y축에 각각 생성해주었다.
이 데이터 분포는 잡음(noise)가 섞여있긴 하지만 (-3, -5)와 (4,15)로 이어지는 하나의 직선이 이 데이터셋을
잘 표현하는 모델일 것이다.
선형 회귀 모델은 다음과 같이 표현될 수 있다.

각각 특성과 그 특성에 대한 가중치의 합과 편항(bias)를 더하여 입력 셋에 대한 예측값을 출력한다.
이를 가설함수(hypothesis function)이라 부른다.
선형회귀의 목적은 이 가설함수를 최대한 실제값과 비슷하게 추정할 수 있도록 가중치와 편향을 업데이트하는 것이다!
선형 회귀 모델에서는 평균 제곱 오차(MSE)를 성능 측정 지표로서 널리 사용한다.
선형 회귀 모델을 훈련시키면 이 MSE를 최소화하는 방향으로 가중치와 편향이 업데이트 된다.
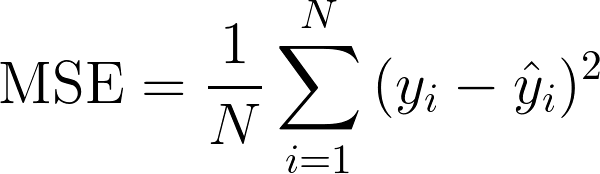
N개의 샘플 각각에 대한 추정치와 실제값 간 차이를 제곱한 것의 총합을 샘플 수(N)로 나눈 평균값을 MSE라 한다.
'좋은 모델'이라 함은, 추정치와 실제값과의 차이를 최소화시켜야한다.
머신러닝에서는 이와 같은 함수를 비용 함수라 한다.
'Machine Learning' 카테고리의 다른 글
| 3-1. 규제 - 릿지 회귀(Ridge Regression) (0) | 2021.04.27 |
|---|---|
| 2-2. 학습 곡선(Learning Curve) (0) | 2021.04.27 |
| 2-1. 다항 회귀(Polynomial Regression) (0) | 2021.04.26 |
| 1-3. 경사 하강법(Gradient descent) - 확률적 경사 하강법(SGD), 미니배치 경사 하강법 (0) | 2021.04.26 |
| 1-2. 경사 하강법(Gradient Descent) - 배치 경사 하강법 (0) | 2021.04.26 |