1-2. 경사 하강법(Gradient Descent) - 배치 경사 하강법

 

선형 회귀를 훈련시킬 수 있는 대표적인 방법 중 하나가 경사 하강법(Gradient Descent)이다. 

 

경사 하강법은 비용 함수를 최소화하는 방향으로 가중치와 편향을 업데이트한다. 

 

이렇게 비용함수를 최소화하는 모델 파라미터의 조합을 찾는 과정을 

 

'모델의 파라미터 공간에서 찾는다'라고 한다. 

 

미분함수가 0이 되는 지점이 최소값임을 나타내고 있다

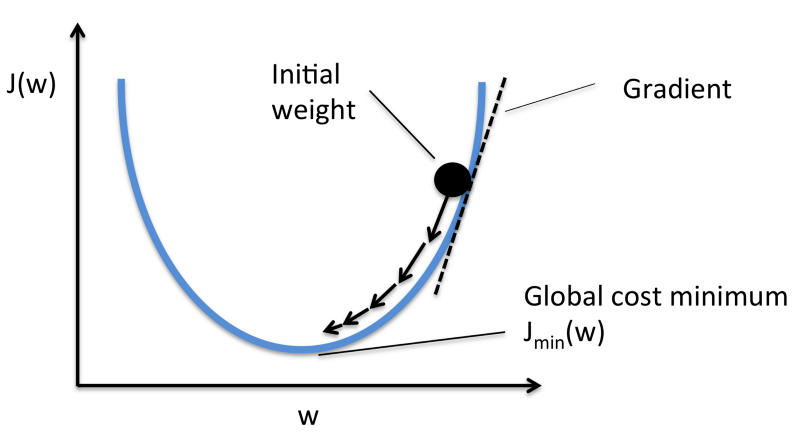
출처 : arahna.de/gradient-descent/

 

미적분의 기본적인 개념으로, 주어진 구간 안에서

 

f(x)를 미분하여 f'(x) = 0 이 되는 지점의 x에서의 f(x)이 최대값, 최소값이 된다. 

 

경사 하강법도 이와 같은 원리를 동일하게 적용한다. 

 

경사 하강법에는 크게 배치 경사 하강법, 확률적 경사 하강법으로 나뉘어진다. 

 

 

 

 

배치 경사 하강법

---

 

 

선형 회귀 모델

내가 추정하고자 하는 선형 모델이 위와 같다면, 찾고자 하는 파라미터는 a와 b이다.

 

주어진 샘플은 x = [1, 2, 3, 4, 5]  y = [7, 10, 13, 16, 19] (실제로 a와 b는 3과 4)라고 가정하자. 

 

x = np.array([1, 2, 3, 4, 5])
y = np.array([7, 10, 13, 16, 19])
plt.scatter(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.show()

추정하고자 하는 선형모델

 

배치 경사하강법에서 먼저 이 가중치를 무작위 초기화한다. ( ex) a = 20, b = 10)

 

theta = [10, 20]
x_b = np.c_[np.ones((len(x),1)),x]
y_hat = x_b.dot(theta)
plt.scatter(x,y_hat,c='red')
plt.show()

 

초기화된 가설함수에서는 x에 대응하여 [ 30.  50.  70.  90. 110.]를 출력한다. 

아직은 실제값과의 차이가 많이 난다. 이를 배치 경사 하강법으로 해결해보도록 하겠다. 

선형 회귀의 비용함수 MSE

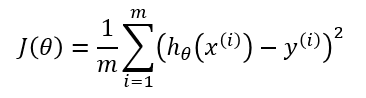
1-1장에서 살펴봤듯이, MSE는 선형회귀에서 사용하는 비용함수이다. 

 

비용함수는 샘플별로 각 샘플별로 예측값이 얼마나 많은 비용을 치뤘는지(얼마나 틀린 값을 예측했는지)를 계산하고,

 

훈련시킨 데이터셋의 크기로 나눠 오차의 평균을 계산한다.

 

 

MSE를 특정 가중치(파라미터)로 미분한 식

 

그레디언트 벡터(모든 파라미터에 일반화)

 

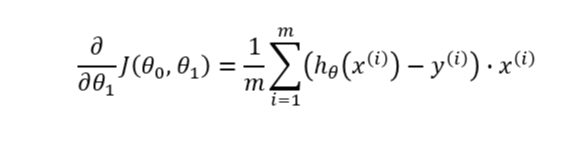
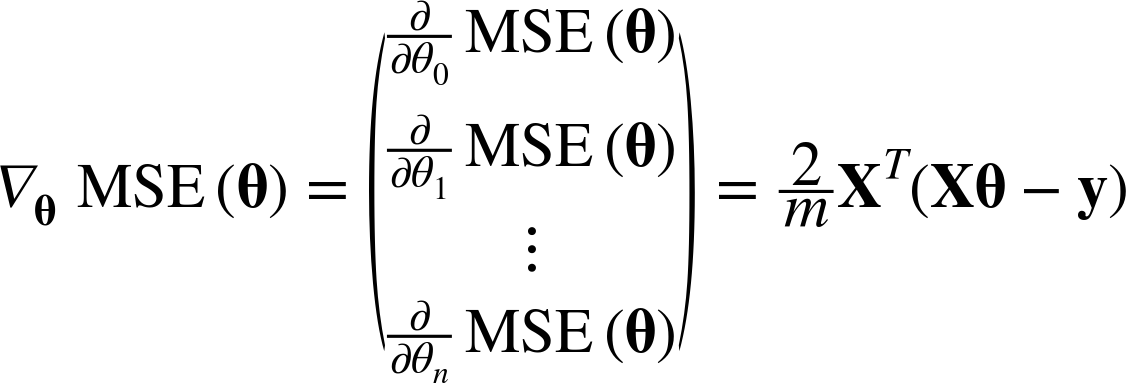
이를 각 파라미터에 대해서 미분한 것이 비용함수의 그레디언트 벡터인데,

 

위의 첫번째 수식에서 나타나듯이 예측값과 타깃값의 차이에 전체 샘플(x)이 행렬곱된다. 

 

def gradient_cost_fun(x_b, y, y_hat):
    diff = y_hat - y
    gradient_cost = x_b.T.dot(diff)*2/len(x)
    return gradient_cost

 

따라서 MSE의 그레디언트 벡터는 [파라미터 개수, 1] 크기의 배열을 반환한다. 

 

정리해서 말하자면, 배치 경사 하강법에서는 같은 가중치가 전체 샘플에 적용되고, 이에 따른 예측값과 타깃값의 차이를 

 

계산한 뒤, 전체 샘플과 곱하여 파라미터 별로 얼마나 실제 파라미터와 차이가 있는지를 반환한다. 

 

이 괴리만큼을 이전 파라미터에서 차감한다. 다시 전체 샘플에 적용하고, 위의 과정을 반복한다. 

 

경사 하강법의 파라미터 업데이트 과정

학습률은 MSE 그레디언트에 곱하는데, 파라미터 업데이트의 정도를 결정하는 하이퍼파라미터이다. 

 

계산한 파라미터가 정답에서 멀수록 그레디언트 벡터는 큰 값의 벡터를 반환하여

 

파라미터 업데이트가 sharply하게 일어날 것이고

 

정답에 근접할수록 그레디언트 벡터는 작은 값을 반환하여 파라미터 업데이트는 작게 일어난다. 

eta = 0.05
n_iteration = 100
gradient_cost_list = []
iter_list = []
for i in range(n_iteration):
    theta = theta - eta * gradient_cost_fun(x_b, y, y_hat)
    y_hat = x_b.dot(theta) #예측값을 업데이트 해준다
    gradient_cost_list.append(gradient_cost_fun(x_b, y, y_hat))
    iter_list.append(i)

 

MSE gradient 값

반복을 거듭할수록 MSE의 gradient 값이 0에 근접해진다

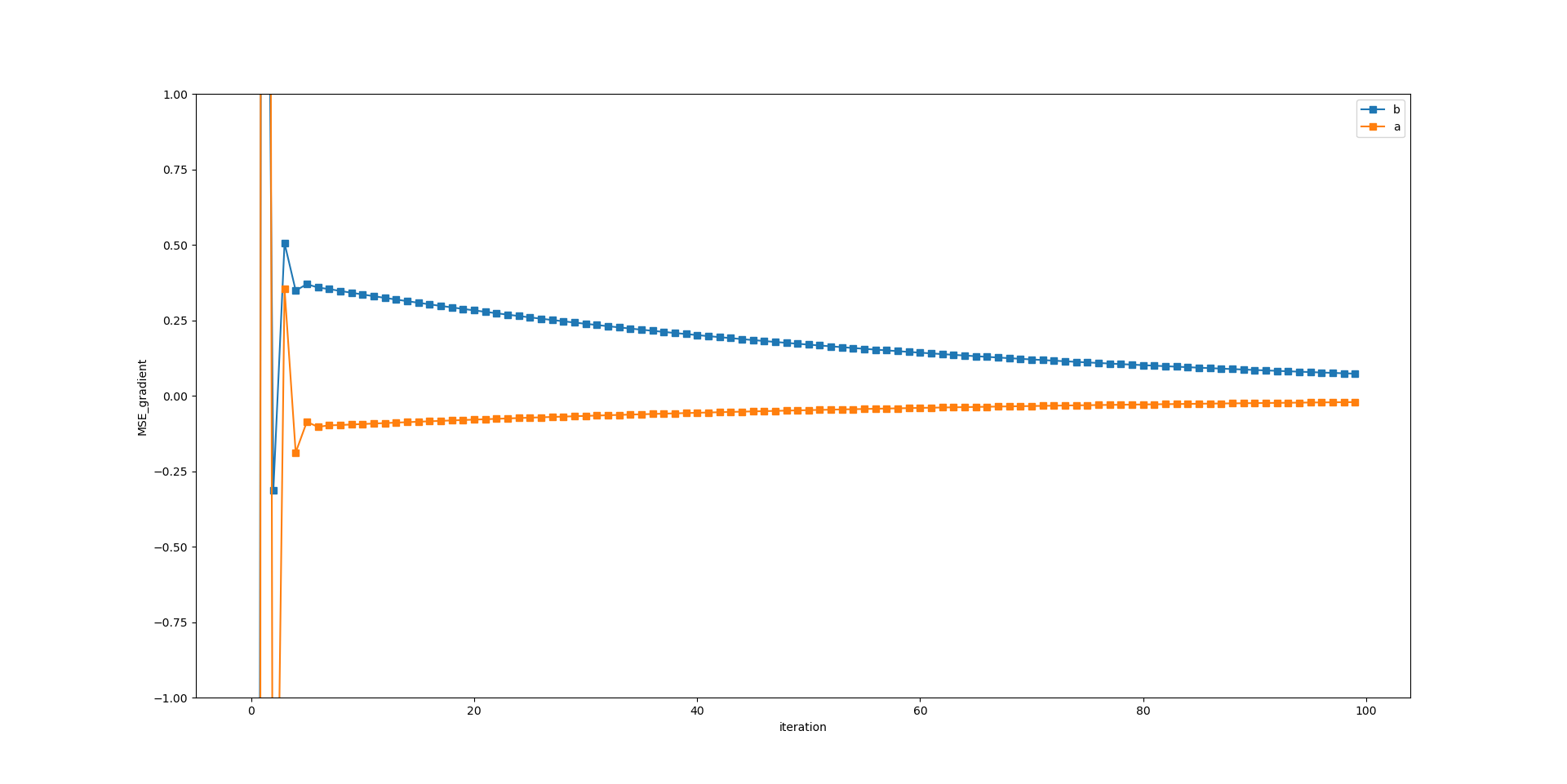
[4.21800789 2.93961531]

타깃값인 b = 4, a =3 에 거의 근접했다. 

 

타깃값 그래프와 거의 일치하는 것을 확인할 수 있다