2-1. 다항 회귀(Polynomial Regression)
2021. 4. 26. 22:09ㆍMachine Learning
1장에서는 선형 데이터를 추정하는 방법을 살펴보았다.
다항 회귀는 비선형 데이터를 선형 모델을 통해 추정하는 기법이다.
먼저 각 특성의 거듭제곱을 (기존 특성과 함께) 새로운 특성으로 추가하고, 이를 선형 모델로 훈련시키는 원리이다.
먼저 샘플을 생성한다.
m = 100
X = 6*np.random.rand(m,1) - 3
y = 0.5*X**2 + X + 2 + np.random.rand(m,1)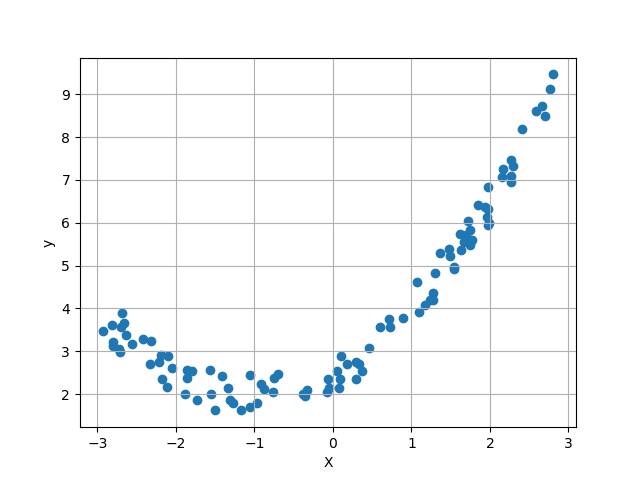
from sklearn.preprocessing import PolynomialFeatures
poly_feather = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_feather.fit_transform(X)사이킷런의 PolynomialFeatures를 통해 특성을 확장한다.
degree는 2로 설정하여 특성의 제곱만을 새 특성으로 추가한다.
print(X_poly[4])
[-1.30577127 1.70503862]분석하고자 하는 데이터셋은 특성값이 하나의 X값이다.
PolynomialFeatures을 통해 기존 특성(X값)의 제곱이 새 특성으로 추가되었다.
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_poly,y)
print(lin_reg.intercept_, lin_reg.coef_)
[2.55036371] [[0.99086344 0.49497576]]
새 특성을 추가한 모델에 선형 회귀를 적용하여 파라미터를 도출한 결과이다.
타깃 파라미터인 [2, 1, 0.5]와 근접하다.
이제 훈련시킨 모델에 테스트 데이터셋을 입력해보자
X_test = np.array([[-6],[-5],[-4],[4],[5],[6]])
print(X_test)
X_test_poly = poly_feather.fit_transform(X_test)
y_hat = lin_reg.predict(X_test_poly)테스트 데이터에 다항 특성을 추가해준뒤, 선형회귀 모델로 예측해보았다.
plt.scatter(X,y)
plt.scatter(X_test,y_hat,c='red')
plt.xlabel('X')
plt.ylabel('y')
plt.grid()
plt.show()
이처럼 다항 모델 역시 다항 특성을 추가함으로써
기존 선형 회귀 모델을 통해 분석이 가능하다는 사실을 알아보았다.
'Machine Learning' 카테고리의 다른 글
| 3-1. 규제 - 릿지 회귀(Ridge Regression) (0) | 2021.04.27 |
|---|---|
| 2-2. 학습 곡선(Learning Curve) (1) | 2021.04.27 |
| 1-3. 경사 하강법(Gradient descent) - 확률적 경사 하강법(SGD), 미니배치 경사 하강법 (1) | 2021.04.26 |
| 1-2. 경사 하강법(Gradient Descent) - 배치 경사 하강법 (0) | 2021.04.26 |
| 1-1. 선형 회귀(Linear regression) (0) | 2021.04.26 |