2023. 8. 3. 22:56ㆍAlgorithm
그래프에서 최단 경로를 찾는 방법은 대표적인 알고리즘 문제 중의 하나이다.
그 중 하나가 벨만-포드(Bellman-Ford) 알고리즘이다.
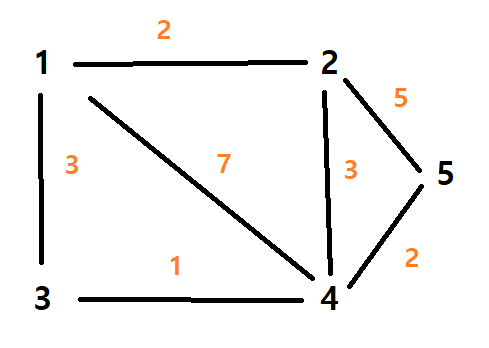
위와 같은 형태의 그래프가 있다고 했을 때, 노드 1에서 노드 4까지 가는 최단 경로는 노드 3을 거치면 4가 된다.
벨만 포드 알고리즘을 노드 갯수-1 크기 만큼의 라운드를 순회하여 특정 노드에서 나머지 노드들까지의
최단 경로를 찾는 알고리즘이다.
typedef vector<tuple<int, int, int>> vecTup;
void bellmanFord(vecTup grap, vi& distance, int start){
for (int i = 0; i < distance.size(); i++) {
distance[i] = 100;
}
distance[start] = 0;
for (int i = 0; i < distance.size() - 1; i++) {
for (auto e : grap) {
int a, b, w;
tie(a, b, w) = e;
cout << "from: "<< a <<" to: "<< b << " weight: " << w << "\n";
distance[b] = min(distance[b], distance[a] + w);
cout << "new distance(from "<<start<<")" << "[" << b << "]: " << distance[b] << "\n\n";
}
}
}그래프의 각 요소는 {시작 노드, 이웃 노드, 가중치} 의 형태로 구성되어 있다.
bellmanFord 는 입력 값으로 그래프 정보, 각 노드들까지의 최단 경로를 담을 배열(distance), 특정 노드(start)를
받는다.
void initGraph(vecTup& grap) {
grap.push_back({1, 2, 2});
grap.push_back({1, 3, 3});
grap.push_back({1, 4, 7});
grap.push_back({2, 4, 3});
grap.push_back({2, 5, 5});
grap.push_back({3, 4, 1});
grap.push_back({4, 5, 2});
}그래프 정보는 위와 같은 형태로 생성한다.
for (int i = 0; i < distance.size(); i++) {
distance[i] = 100;
}가장 먼저 특정 노드(start)에서 각 노드까지의 길이를 임의의 큰 값으로 초기화한다.
distance[start] = 0;그리고 자신까지의 길이는 0으로 설정한다.
for (int i = 0; i < distance.size() - 1; i++) {
for (auto e : grap) {
int a, b, w;
tie(a, b, w) = e;
distance[b] = min(distance[b], distance[a] + w);
}
}그리고 노드의 수 - 1 크기의 라운드만큼 반복하면서 각 노드까지의 최단 거리를 갱신해나간다.
처음에 시작 노드(start)와 직접 이웃인 노드들(b라고 했을 때)은 distance[b]의 최초 길이(100)보다
distance[a](0)에 가중치 w를 더한 것이 작기 때문에 가중치 크기(start와 이웃노드까지의 길이)로 갱신된다.
start 노드와 직접 이웃 노드가 아니라면 갱신은 이루어지지 않는다.
두번째 라운드부터 갱신이 이루어지는데, start 노드와 직접 이웃인 노드들을 통해서 경유했을 때 더 짧은지
살펴보고 경유하는 경우가 더 짧다면 노드 a를 경유하도록 갱신된다.
결과적으로 모든 라운드를 순회했을 때 distance에는 start노드로부터 각 노드까지의 최단 거리가 저장된다.
아래는 거리 갱신 과정을 보여준다.
from: 1 to: 2 weight: 2
new distance(from 1)[2]: 2
from: 1 to: 3 weight: 3
new distance(from 1)[3]: 3
from: 1 to: 4 weight: 7
new distance(from 1)[4]: 7
from: 2 to: 4 weight: 3
new distance(from 1)[4]: 5
from: 2 to: 5 weight: 5
new distance(from 1)[5]: 7
from: 3 to: 4 weight: 1
new distance(from 1)[4]: 4
from: 4 to: 5 weight: 2
new distance(from 1)[5]: 6
-------------0th ROUND END--------------
from: 1 to: 2 weight: 2
new distance(from 1)[2]: 2
from: 1 to: 3 weight: 3
new distance(from 1)[3]: 3
from: 1 to: 4 weight: 7
new distance(from 1)[4]: 4
from: 2 to: 4 weight: 3
new distance(from 1)[4]: 4
from: 2 to: 5 weight: 5
new distance(from 1)[5]: 6
from: 3 to: 4 weight: 1
new distance(from 1)[4]: 4
from: 4 to: 5 weight: 2
new distance(from 1)[5]: 6
-------------1th ROUND END--------------
from: 1 to: 2 weight: 2
new distance(from 1)[2]: 2
from: 1 to: 3 weight: 3
new distance(from 1)[3]: 3
from: 1 to: 4 weight: 7
new distance(from 1)[4]: 4
from: 2 to: 4 weight: 3
new distance(from 1)[4]: 4
from: 2 to: 5 weight: 5
new distance(from 1)[5]: 6
from: 3 to: 4 weight: 1
new distance(from 1)[4]: 4
from: 4 to: 5 weight: 2
new distance(from 1)[5]: 6
-------------2th ROUND END--------------
from: 1 to: 2 weight: 2
new distance(from 1)[2]: 2
from: 1 to: 3 weight: 3
new distance(from 1)[3]: 3
from: 1 to: 4 weight: 7
new distance(from 1)[4]: 4
from: 2 to: 4 weight: 3
new distance(from 1)[4]: 4
from: 2 to: 5 weight: 5
new distance(from 1)[5]: 6
from: 3 to: 4 weight: 1
new distance(from 1)[4]: 4
from: 4 to: 5 weight: 2
new distance(from 1)[5]: 6
-------------3th ROUND END--------------
from: 1 to: 2 weight: 2
new distance(from 1)[2]: 2
from: 1 to: 3 weight: 3
new distance(from 1)[3]: 3
from: 1 to: 4 weight: 7
new distance(from 1)[4]: 4
from: 2 to: 4 weight: 3
new distance(from 1)[4]: 4
from: 2 to: 5 weight: 5
new distance(from 1)[5]: 6
from: 3 to: 4 weight: 1
new distance(from 1)[4]: 4
from: 4 to: 5 weight: 2
new distance(from 1)[5]: 6
-------------4th ROUND END--------------'Algorithm' 카테고리의 다른 글
| [알고리즘/C++] 플로이드-워셜(Floyd-Warshall) 알고리즘 (0) | 2023.08.03 |
|---|---|
| [알고리즘/C++] 다익스트라 알고리즘(Dijkstra's Algorithm) (0) | 2023.08.03 |
| [알고리즘/C++] 그래프 순회 - 너비 우선 탐색(BFS) (0) | 2023.08.03 |
| [알고리즘/C++] 그래프 순회 - 깊이 우선 탐색(DFS) (0) | 2023.08.03 |
| [알고리즘/C++] 동적 계획법 - 엘리베이터 운행횟수 (0) | 2023.07.29 |