2023. 8. 3. 23:35ㆍAlgorithm
다익스트라 알고리즘은 벨만 포드 알고리즘과 같이 특정 노드로부터 다른 노드들까지의 최단 거리를 계산하는
알고리즘으로, 벨만 포드보다 더 효율적이로 대중적으로 쓰이는 알고리즘이다.
다익스트라의 기본 메커니즘은 다음과 같다.
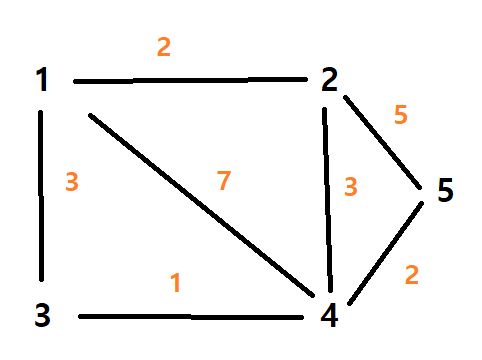
위 그래프에서 노드 1을 기준으로 각 노드까지의 최단 거리를 찾는다고 할 때,
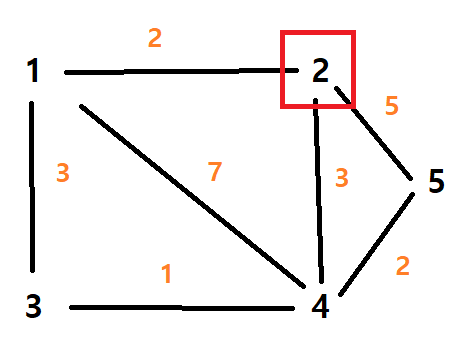
노드 1에서 가장 가까운 노드는 거리 2를 가진 노드 2이다. 초점은 노드 2로 옮겨간다.
노드 2까지의 거리는 2이다.
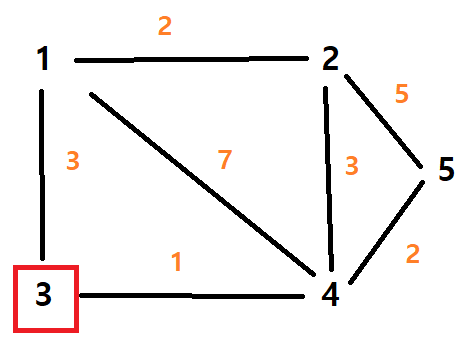
노드 2를 방문했으니
나머지 노드들 중에 1과 가장 가까운 노드는 노드 3이다. 노드3까지의 거리는 3으로 갱신된다.
우선순위 큐에 노드 3에 대한 갱신 정보를 넣어준다.
노드 3의 이웃 노드들까지 시야를 확대해서 나머지 노드들 중 가장 가까운 노드를 찾는다.
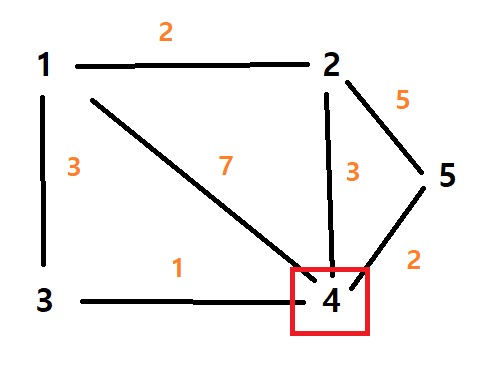
노드 4는 노드 3을 경유함으로써 가장 짧은 경로가 생성된다.
초점은 노드 4로 옮겨간다.

노드 4를 경유해서 노드 5로 가는 더 짧은 경로를 발견했다. 초점은 노드 5로 옮겨간다.
이런 식으로 각 노드들간의 최단 경로 길이를 갱신해나간다.
typedef priority_queue<pair<int, int>> pqDisNod;
void dijkstra(vi& distance,vector<vector<pair<int, int>>> adj, int start) {
for (int i = 0; i < distance.size(); i++) {
distance[i] = 100;
}
pqDisNod pq;
vi visited(100, 0);
distance[start] = 0;
pq.push({0, start});
while (!pq.empty()) {
int a = pq.top().second;
pq.pop();
//가장 짧은 거리의 경우를 pop
if (visited[a]) {
continue;
}
visited[a] = 1;
for (int i = 0; i < adj[a].size(); i++) {
// a에 연결된 노드 모두 살펴본다
int b = adj[a][i].first;
// a와 연결된 한 노드
int w = adj[a][i].second;
// a에서 b까지의 거리
if (distance[b] > distance[a] + w) {
// a를 거쳐서 가는 게 더 빠르면
distance[b] = distance[a] + w;
// a를 거치는 경로의 거리로 갱신
pq.push({ -distance[b], b });
// 갱신된 거리를 우선순위 큐에 넣기
}
}
}
}
위는 다익스트라 알고리즘의 전체 코드이다.
typedef priority_queue<pair<int, int>> pqDisNod;다익스트라에서 사용하는 우선순위 큐의 형태이다. 각 요소에는 <int,int>의 pair가 들어가는데
{-노드까지의 길이, 노드번호} 로 들어가는데, 알고리즘 상 가장 가까운 노드를 찾아야하기 때문에
최대값을 찾는 우선순위 큐 특성 상 일부러 길이에 '-' 를 취하였다.
for (int i = 0; i < distance.size(); i++) {
distance[i] = 100;
}먼저 각 노드까지의 길이를 임의의 큰 값으로 초기화한다.
pqDisNod pq;
vi visited(100, 0);
distance[start] = 0;
pq.push({0, start});우선순위 큐를 선언하고, 방문 기록을 남기기 위해 visited 배열을 선언한다.
distance에 시작노드와의 거리를 0으로 넣어주고, 우선순위 큐에 들어가는 최초 값은 {0, 시작노드}이다.
while (!pq.empty()) {
int a = pq.top().second;
pq.pop();
//가장 짧은 거리의 경우를 pop
if (visited[a]) {
continue;
}
visited[a] = 1;우선순위 큐의 가장 top 값(시작 노드와 가장 가까운 노드)을 pop하고 이미 방문한 노드이면 넘기고
처음 방문이면 방문 기록을 남긴다.
for (int i = 0; i < adj[a].size(); i++) {
// a에 연결된 노드 모두 살펴본다
int b = adj[a][i].first;
// a와 연결된 한 노드
int w = adj[a][i].second;
// a에서 b까지의 거리
if (distance[b] > distance[a] + w) {
// a를 거쳐서 가는 게 더 빠르면
distance[b] = distance[a] + w;
// a를 거치는 경로의 거리로 갱신
pq.push({ -distance[b], b });
// 갱신된 거리를 우선순위 큐에 넣기
}
}그리고 해당 노드(우선순위 큐에서 pop한 노드, a)의 직접 이웃 노드와 그 거리를 살펴보고, 해당 노드(a)를 거쳐서
이 노드의 직접 이웃 노드(b)를 가는 것이 더 빠르면 경유한 거리로 갱신한다.
갱신이 이루어지면 새로운 거리(를 음수화)와 그 목적지 노드를 우선순위 큐에 저장한다.
while문이 반복되면서 우선순위 큐의 top값을 pop하기 때문에 항상 초점은 start 노드에서
(방문이 아직 안된 노드들 중에) 가장 가까운 노드로 갱신된다.
우선순위 큐가 빌 때까지 해당 과정을 반복하면 결국 distance에는 각 노드까지의 최단 거리가 저장된다.
vector<vector<pair<int, int>>> adj;
//each node has several (neighbor, weight) pair.
initGraph3(adj);
//make adjacent matrix
vi distance(5, 0);
distance.insert(distance.begin(), 0);
//insert sentinel value
dijkstra(distance, adj, 1);
//calculate the shortest distance from node 16 0 2 3 4 6
// 0번째 값은 sentinel value에 의한 값'Algorithm' 카테고리의 다른 글
| [알고리즘/C++] 플로이드(Floyd) - 그래프 내에서 사이클 찾기 (0) | 2023.08.04 |
|---|---|
| [알고리즘/C++] 플로이드-워셜(Floyd-Warshall) 알고리즘 (1) | 2023.08.03 |
| [알고리즘/C++] 최단 경로 찾기 - 벨만-포드 알고리즘(Bellman-Ford) (0) | 2023.08.03 |
| [알고리즘/C++] 그래프 순회 - 너비 우선 탐색(BFS) (0) | 2023.08.03 |
| [알고리즘/C++] 그래프 순회 - 깊이 우선 탐색(DFS) (0) | 2023.08.03 |