8-2. PCA(Principal Component Analysis)
2021. 5. 12. 20:17ㆍMachine Learning
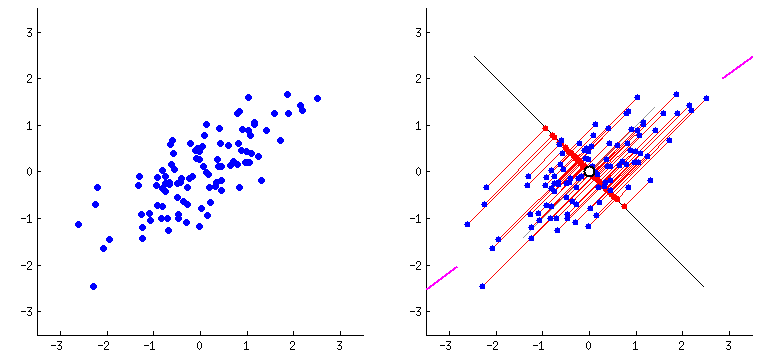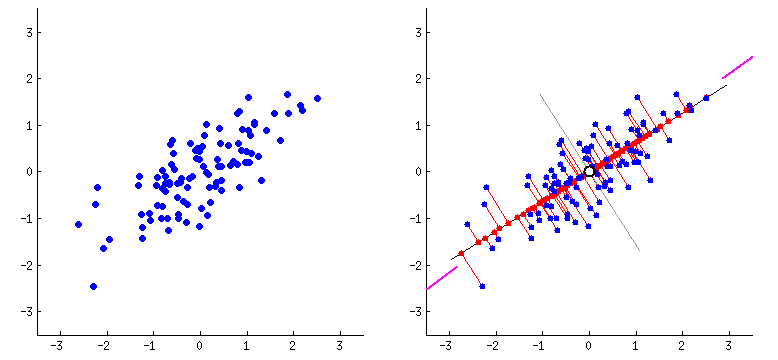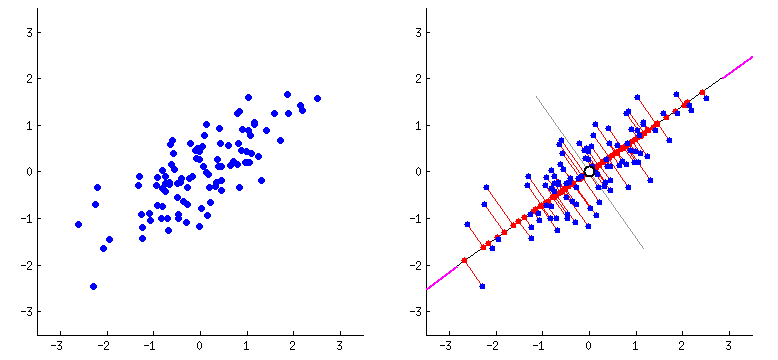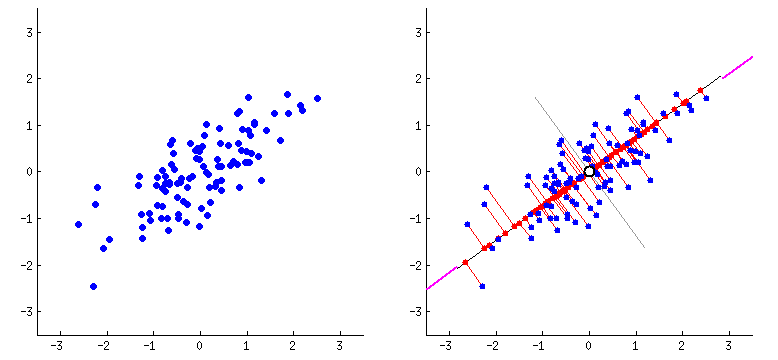
주성분 분석(Principal Component Analysis, PCA)는 데이터에 가장 가까운 초평면을 정의하고,
이 초평면에 데이터를 투영시키는 기법이다.
출처 : laptrinhx.com/dimensionality-reduction-principal-component-analysis-359354885/
위 그림은 투영시켰을 때 데이터셋과의 평균제곱거리가 가장 적은 초평면을 찾고 투영시키는 과정을 나타냈다.
PCA의 과정은 다음과 같다.

출처 : medium.com/xebia-engineering/principal-component-analysis-autoencoder-257e90d08a4e
1. 데이터셋의 분산을 최대한 보존하는 축을 찾는다. (1번째 주성분)
2. 1번째 주성분에 직교하고, 남은 분산을 최대한 보존하는 축을 찾는다. (2번째 주성분)
.
.
.
n. 1 ~ n-1번째 주성분에 직교하고, 남은 분산을 최대한 보존하는 축을 찾는다. (n번째 주성분)
데이터셋의 주성분은 특이값 분해(SVD)라는 기법을 통해 찾는다.
특이값 분해에서는 데이터셋 X를 UΣV^t 로 분해한다. 모든 주성분의 단위 벡터는 V^t에 담겨있다.

출처 : Hands On Machine Learning 2판, Aurélien Géron
위 그림은 3차원 데이터셋의 2가지 주성분을 찾고 이 두 주성분으로 평면을 형성하여 투영시킨 결과이다.

기존 데이터셋 X와 d개의 주성분 벡터를 담은 행렬 W_d를 행렬곱셈하여 투영된 X_d-proj를 계산할 수 있다.
반대로 기존 주성분 벡터 행렬을 전치한 행렬을 투영한 데이터와 행렬곱하여 다시 복원할 수 있다.

재구성된 데이터와 원본 데이터 사이의 오차를 재구성 오차라고 한다.
커널 PCA
샘플에 커널 트릭을 적용하여 고차원 공간에 매핑하고 선형 분류(회귀)할 경우, 원본 데이터에서의 비선형 분류(회귀)를
가능한다. 이 기법을 PCA에도 동일하게 적용하여 차원 축소를 위한 비선형 투영을 가능하게한 것이 커널 PCA이다.

출처 : scikit-learn.org/stable/auto_examples/decomposition/plot_kernel_pca.html
'Machine Learning' 카테고리의 다른 글
| 9-2. 군집(Clustering) - K평균 클러스터링(2) (0) | 2021.05.20 |
|---|---|
| 9-1. 군집(Clustering) - K평균 클러스터링(1) (1) | 2021.05.20 |
| 8-1. 차원 축소(Dimensionality Reduction) (0) | 2021.05.12 |
| 7-5. 부스팅(Boosting) - 그레이디언트 부스팅(Gradient Boosting) (1) | 2021.05.12 |
| 7-4. 부스팅(Boosting) - 에이다부스트(Adaboost) (0) | 2021.05.12 |