2021. 5. 20. 01:34ㆍMachine Learning
이전 장에서는 샘플마다 레이블링이 되어있는 데이터셋에 대해 살펴보았다.
비지도 학습은 레이블이 없는 데이터를 분류하는 알고리즘이다.
비지도 학습에는 크게 군집(Clustering), 이상치 탐지(Outlier Detection), 밀도 추정(Density estimation)이 있다.
군집(Clustering)
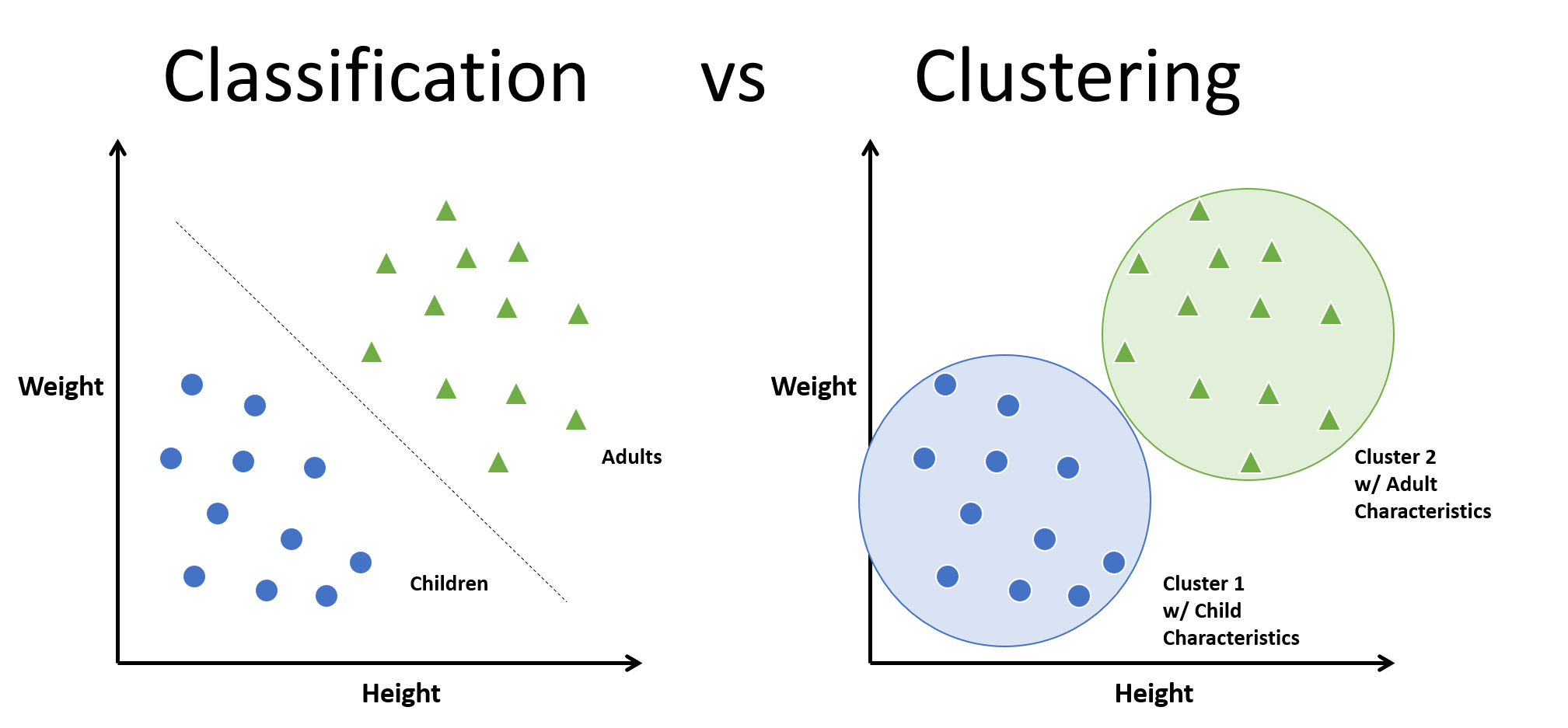
출처 : https://kevin-c-lee26.medium.com/machine-learning-101-classification-vs-clustering-e11b12c71243
군집(Clustering)이란 데이터셋에서 비슷한 샘플들을 하나의 클러스터 또는 비슷한 샘플의 그룹으로 할당하는 작업이다.
대표적인 군집 알고리즘으로 K-mean 클러스터링과 DBSCAN이 있다.
K-mean 클러스터링
K-mean 클러스터링은 각 클러스터의 센트로이드를 찾고 센트로이드 중심으로 샘플들을 클러스터링하는
기법이다.
from sklearn.cluster import KMeans
sample_n = 50
rows = 5
columns = sample_n
total_sample = sample_n*rows
X = [[0 for _ in range(rows)] for _ in range(columns)]
Y = [[0 for _ in range(rows)] for _ in range(columns)]클러스터를 임의로 생성시켜주기 위해 각 클러스터 당 샘플 50개씩, 총 5개의 클러스터를 생성하기 위해
2차원 배열을 0으로 채웠다.
for idx in range(rows):
variance = abs(np.random.randn(1)*3)
trans_x = np.random.randn(1)*10
trans_y = np.random.randn(1)*10
X[idx] = np.random.randn(sample_n)*variance + trans_x
Y[idx] = np.random.randn(sample_n)*variance + trans_y
X_new = np.concatenate([X[0], X[1], X[2], X[3], X[4]], axis=0)
Y_new = np.concatenate([Y[0], Y[1], Y[2], Y[3], Y[4]], axis=0)
cluster_set = np.zeros((total_sample,2))
for idx in range(len(cluster_set)):
cluster_set[idx][0] = X_new[idx]
cluster_set[idx][1] = Y_new[idx]
np.random.shuffle(cluster_set)클러스터의 분산을 지정해주고 randn 함수를 통해 생성된 임의의 값을 중심으로 X, Y 값을 생성하였다.
각 클러스터를 이어붙여준 뒤에 전체 클러스터의 모든 샘플들을 한 2차원 배열 객체에 모았다.
kmeans = KMeans(n_clusters=5)
y_pred = kmeans.fit_predict(cluster_set)
print(y_pred)KMeans 객체를 생성하여 총 5개의 클러스터로 나눌 것을 명시하고, 생성한 훈련세트로 훈련시킨 뒤에 예측하였다.
[0 4 1 2 0 3 1 3 2 3 1 2 4 2 3 3 1 1 3 4 0 1 4 0 4 2 1 0 2 0 0 0 0 4 2 2 4
1 1 1 1 1 0 2 0 0 2 0 2 3 0 0 2 1 1 1 4 4 0 4 3 2 1 0 0 0 4 1 3 4 0 3 0 1
4 4 3 0 2 3 3 0 3 2 4 3 1 1 4 3 0 4 2 0 2 1 1 2 0 3 4 0 2 0 2 1 2 0 1 2 4
2 1 4 2 0 0 1 1 1 1 3 4 1 3 4 1 4 0 2 3 2 0 0 1 0 2 4 3 2 4 0 2 2 1 2 0 4
0 2 3 4 3 1 3 1 1 4 0 2 4 4 4 2 1 2 4 3 4 1 3 0 3 2 4 3 2 2 4 4 4 0 3 3 3
2 2 1 0 1 4 0 1 2 3 4 2 3 4 0 4 4 3 3 2 4 4 1 3 1 3 2 3 2 0 0 4 1 2 2 1 0
2 1 0 3 1 1 4 3 0 4 0 0 3 3 0 4 1 2 2 1 3 2 0 0 4 4 2 0]각 샘플에 붙여진 레이블이며, 이는 kmean.labels_를 통해서 확인할 수 있다.
print(kmeans.labels_[0]) #KMean 클러스터링이 첫번째 샘플을 레이블링한 값
0이는 훈련된 Kmean 인스턴스에 의해 예측값이며, 해당 샘플의 진짜 레이블을 의미하지는 않는다.

color_dic = {0: 'red', 1: 'orange',2: 'yellow', 3: 'green',4: 'blue'}
for idx in range(len(cluster_set)):
color_idx = kmeans.labels_[idx]
plt.scatter(cluster_set[idx][0], cluster_set[idx][1], c=color_dic[color_idx])
plt.xlabel('X')
plt.ylabel('Y')
for idx in range(len(kmeans.cluster_centers_)):
plt.scatter(kmeans.cluster_centers_[idx][0],kmeans.cluster_centers_[idx][1], c='black')
#센트로이드는 따로 검정색 마크로 표시클러스터링이 적절히 이뤄졌는지 확인하기 위해서 레이블별 색상을 딕셔너리 형태로 저장한 후
scatter 그래프로 확인해보았다.

적절히 클러스터링된 것을 확인할 수 있다. 이렇게 각 샘플에 특정 레이블을 부여하는 것을 하드 군집이라고 한다.
반면에 샘플 별로 각 레이블의 확률을 부여하는 방식을 소프트 군집이라고 한다.
'Machine Learning' 카테고리의 다른 글
| 9-3. 군집(Clustering) - 준지도 학습 (2) | 2021.05.21 |
|---|---|
| 9-2. 군집(Clustering) - K평균 클러스터링(2) (0) | 2021.05.20 |
| 8-2. PCA(Principal Component Analysis) (1) | 2021.05.12 |
| 8-1. 차원 축소(Dimensionality Reduction) (0) | 2021.05.12 |
| 7-5. 부스팅(Boosting) - 그레이디언트 부스팅(Gradient Boosting) (1) | 2021.05.12 |