2021. 6. 12. 21:48ㆍFinancial Analysis
주식 포트폴리오를 짤 때 전략 없이 종목을 구성하는 것이 아닌, 전략적으로 구성한다면 더 좋은
수익률을 거둘 수 있다. 그러한 지표 중 하나가 효율적 투자선(Efficient Frontier)이다.
What Is Efficient Frontier?The efficient frontier is the set of optimal portfolios that offer the highest expected return for a defined level of risk or the lowest risk for a given level of expected return. Portfolios that lie below the efficient frontier are sub-optimal because they do not provide enough return for the level of risk. Portfolios that cluster to the right of the efficient frontier are sub-optimal because they have a higher level of risk for the defined rate of return.
https://www.investopedia.com/terms/e/efficientfrontier.asp
Efficient Frontier Definition
Efficient frontier comprises investment portfolios that offer the highest expected return for a specific level of risk.
www.investopedia.com
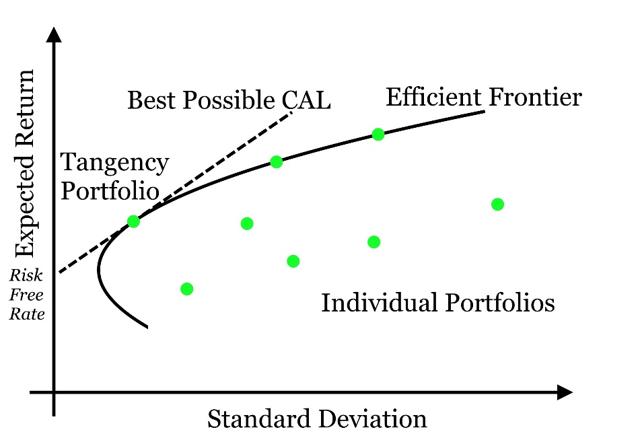
출처 : https://seekingalpha.com/article/4200744-difference-45-percent-return-and-28-efficient-frontier
Investopedia에 따르면, 효율적 투자선이란 정의된 위험 수준에 대한 최고 기대 수익 또는 주어진 기대 수익 수준에 대한
최저 위험율을 제공하는 최적의 포트폴리오 세트이며, 효율적 투자선 내부에 존재하는 포트폴리오 세트에 대해서는
같은 위험률에 대해서 더 낮은 수익을 제공하기 때문에 좋은 선택이 아니다.
지금까지 구현된 MarketDB API를 활용하여 특정 기간 동안의 각 종목의 종가를 가져와서 효율적 투자선을 구해보자.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from Investar.MarketDB import MarketDB
class efficient_frontier:
def __init__(self, stock_list, start_date, end_date):
self.daily_ret = []
self.annual_ret = []
self.daily_cov = []
self.annual_cov = []
self.stocks = pd.DataFrame()
self.port_ret = []
self.port_risk = []
self.port_weight = []
self.calc_indict(stock_list, start_date, end_date)
def calc_indict(self, stock_list, start_date, end_date):
"""종목 리스트와 시작일, 종료일을 인자로 받아 해당 종목들의 일간 수익률, 연간 수익률
일간 리스크, 연간 리스크를 구한다."""
def monte_carlo_sim(self, stock_list):
"""각 종목들의 일간 수익률, 연간 수익률 일간 리스크, 연간 리스크를
바탕으로 많은 수의 랜덤한 포트폴리오를 생성하여 효율적 투자선을 구한다."""효율적 투자선을 구하는 efficient_frontier 클래스이다.
def calc_indict(self, stock_list, start_date, end_date):
mk = MarketDB()
for s in stock_list:
self.stocks[s] = mk.get_daily_price(s, start_date, end_date)['close']
self.daily_ret = self.stocks.pct_change()
self.annual_ret = self.daily_ret.mean()*252
self.daily_cov = self.daily_ret.cov()
self.annual_cov = self.daily_cov * 252
returncalc_indict 함수에서는 종목 리스트와 시작일, 종료일을 인자로 받아 MarketDB API를 통해 각 종목들의 종가를
클래스 멤버인 stocks 데이터프레임에 저장한다.
금호타이어 호텔신라 CJ대한통운 대한항공
date
2018-10-02 NaN NaN NaN NaN
2018-10-04 -0.009728 -0.075122 -0.062112 -0.001835
2018-10-05 -0.007859 0.002110 0.016556 0.018382
2018-10-08 -0.001980 -0.029474 -0.003257 -0.003610
2018-10-10 -0.007937 -0.046638 -0.032680 -0.016304
... ... ... ... ...
2021-04-28 -0.012453 0.021403 -0.002793 0.005660
2021-04-29 0.003783 0.031432 -0.025210 -0.011257
2021-04-30 0.015075 -0.023702 -0.014368 0.020873
2021-05-03 -0.023515 0.031214 -0.023324 -0.018587
2021-05-04 0.012674 0.013453 0.005970 -0.001894
[639 rows x 4 columns]수익률을 비교하기 위해서 각 종목들의 일간 변동률을 구해야한다. 이는 판다스 데이터프레임의 pct_change()함수로
구할 수 있다.
금호타이어 -0.040702
호텔신라 0.032863
CJ대한통운 0.070166
대한항공 0.087604
dtype: float64연간 수익률은 일간 수익률의 평균에서 252(개장일)을 곱해준다.
금호타이어 호텔신라 CJ대한통운 대한항공
금호타이어 0.000470 0.000175 0.000097 0.000237
호텔신라 0.000175 0.000656 0.000129 0.000292
CJ대한통운 0.000097 0.000129 0.000416 0.000125
대한항공 0.000237 0.000292 0.000125 0.000789각 종목 간의 상관관계를 계산하기 위해 일간 공분산은 daily_ret에 cov() 함수를 적용하여 구하고,
금호타이어 호텔신라 CJ대한통운 대한항공
금호타이어 0.118556 0.044151 0.024321 0.059767
호텔신라 0.044151 0.165300 0.032545 0.073674
CJ대한통운 0.024321 0.032545 0.104827 0.031422
대한항공 0.059767 0.073674 0.031422 0.198738연간 공분산도 마찬가지로 252를 곱하여 구한다.
def monte_carlo_sim(self, stock_list):
for _ in range(20000):
weights = np.random.random(len(stock_list))
total_weight = np.sum(weights)
weights /= total_weight
returns = np.dot(weights, self.annual_ret)
risk = np.sqrt(np.dot(weights.T, np.dot(self.annual_cov, weights)))
self.port_ret.append(returns)
self.port_risk.append(risk)
self.port_weight.append(weights)
portfolio = {'Returns' : self.port_ret, 'Risk' : self.port_risk}
for i, s in enumerate(stock_list):
portfolio[s] = [weight[i] for weight in self.port_weight]
portfolio = pd.DataFrame(portfolio)
portfolio.plot.scatter(x='Risk', y='Returns',grid=True)
plt.title("Efficient Frontier")
plt.xlabel('Risk')
plt.ylabel('Expected Returns')
plt.show()
return portfolio몬테카를로 시뮬레이션을 통해 각 종목별로 포트폴리오 비율을 가중치로 설정하여 랜덤하게 생성하고,

출처 : https://financetrain.com/how-to-calculate-portfolio-risk-and-return/
가중치와 연간 수익률과 곱한 값이 전체 포트폴리오의 기대 수익률이다.

출처 : https://quant.stackexchange.com/questions/21572/calculating-portfolio-risk
포트폴리오의 리스크는 연간 공분산과 가중치의 곱을 다시 가중치의 전치행렬과 곱하면 포트폴리오의 위험률이 구해진다.
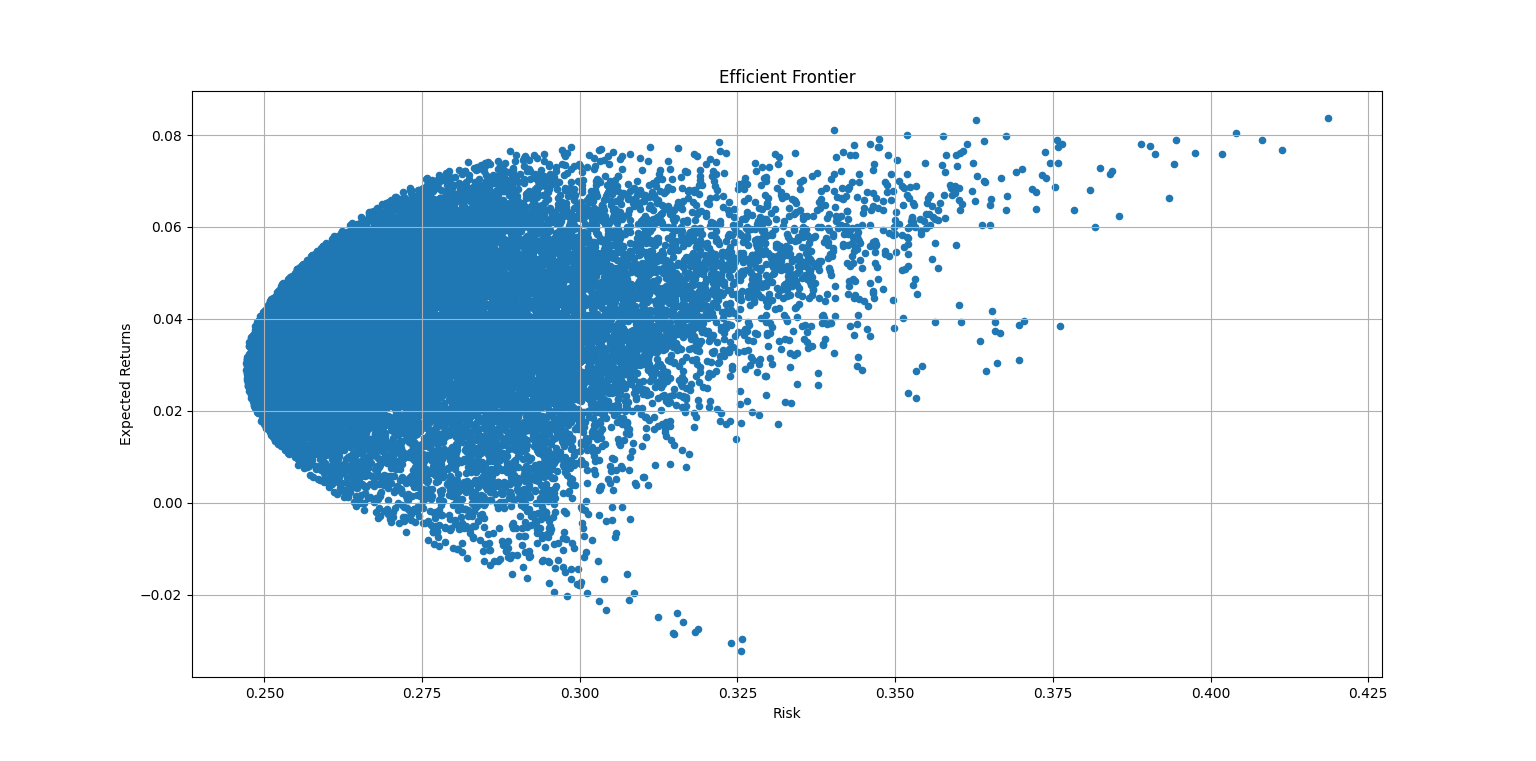
이렇게 Return, Risk, Weight를 포트폴리오마다 저장하여 x축을 Risk로, y축을 Return으로 하는
scatter 그래프를 통해 효율적 투자선을 확인하였다.
'Financial Analysis' 카테고리의 다른 글
| 4-1. [트레이딩 전략 구현] 볼린저 밴드 지표 (2) | 2021.06.13 |
|---|---|
| 3-2. [트레이딩 전략 구현] 샤프 지수(Sharpe Ratio) (0) | 2021.06.12 |
| 2-2. DB에서 시세 조회하는 API 만들기 (0) | 2021.06.06 |
| 2-1. 스크래핑한 데이터를 DB에 저장하기 (2) | 2021.06.05 |
| 1-2. 웹 스크레이핑을 통한 일별 시세 분석하기 (3) | 2021.05.29 |