2021. 9. 10. 22:10ㆍDeep Learning
본 게시글은 한빛미디어 『밑바닥부터 시작하는 딥러닝, 사이토 고키, 2020』의 내용을 참조하였음을 밝힙니다.
이전 장에서는 입력으로부터 출력을 만들어내는 퍼셉트론을 알아보았다.
이번 장에서는 다수의 퍼셉트론을 이용하여 데이터로부터 가중치를 자동으로 학습하는 '신경망(neural network)'이라는
개념에 대해서 알아보도록 한다.
신경망(neural network) 도입
An ANN is based on a collection of connected units or nodes called artificial neurons, which loosely model the neurons in a biological brain. Each connection, like the synapses in a biological brain, can transmit a signal to other neurons. An artificial neuron receives a signal then processes it and can signal neurons connected to it. The "signal" at a connection is a real number, and the output of each neuron is computed by some non-linear function of the sum of its inputs. The connections are called edges. Neurons and edges typically have a weight that adjusts as learning proceeds. The weight increases or decreases the strength of the signal at a connection. Neurons may have a threshold such that a signal is sent only if the aggregate signal crosses that threshold. Typically, neurons are aggregated into layers. Different layers may perform different transformations on their inputs. Signals travel from the first layer (the input layer), to the last layer (the output layer), possibly after traversing the layers multiple times.
출처 : https://en.wikipedia.org/wiki/Artificial_neural_network
신경망의 정의는 위와 같다. 위의 한 문단에서 신경망에 대한 중요한 내용을 모두 담고있는데 직역하자면 다음과 같다.
인공신경망(ANN)은 실제 뇌의 뉴런을 러프하게 모델링한 것이다. 우리 뇌에서는 연결된 부위마다 시냅스를 통해 다른
뉴런으로 신호(signal)을 전달하고, 인공 뉴런에서는 신호를 가공(process)하고 다른 뉴런으로 이를 전달한다.
각 뉴런의 출력(output)은 입력들의 합을 비선형 함수(non-linear)로 처리한다. 각 연결들은 'edge'라고 부르고
이 엣지(edge)마다 가중치(wieght)를 갖는다. 가중치를 학습을 통해 조정되며 연결의 강도를 조절한다.
뉴런은 임계값(threshold)를 가지는데 통합된 신호들(가중치*입력 합)이임계값을 넘었을 때만 신호가 다음 뉴런으로
전달된다.
출처 : https://towardsdatascience.com/whats-the-role-of-weights-and-bias-in-a-neural-network-4cf7e9888a0f
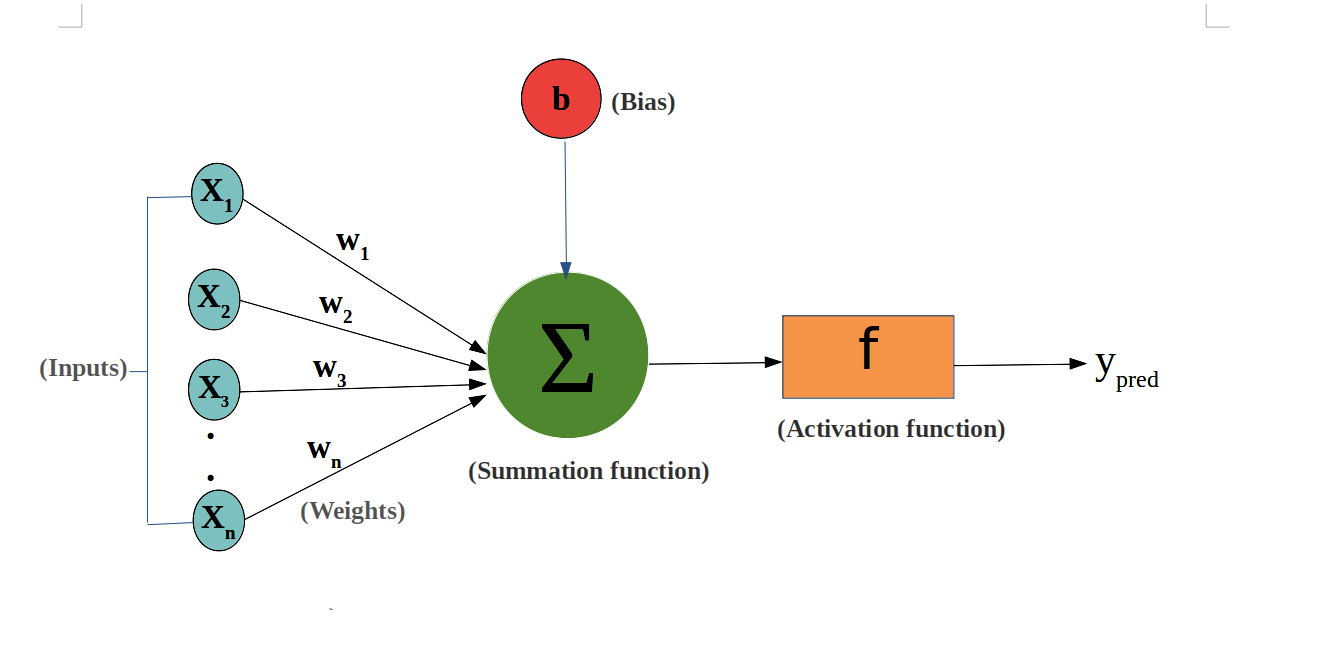
퍼셉트론에 다시 돌아가보면, 각 입력들(x1, x2, x3, ... ,xn)은 가중치(w1, w2, ..., wn)과 곱해지고 임계값의 역할을
수행하는 편향(bias)인 b를 만나 하나의 결과(총합)이 만들어지고 이 총합이 활성화 함수(activation function)을 만나
(다음 뉴런으로 전달할) 최종 출력을 만들어낸다.
가중치(w)는 각 신호(입력)의 영향력을 제어하고, 편향(b)은 뉴런의 활성화 난이도(얼마나 쉽게 활성화되느냐)를
제어한다.
활성화 함수(Activation function)
그렇다면 이전 뉴런들의 계산된 결과들이 거쳐야하는 활성화 함수란 무엇이고, 또 왜 필요한걸까?
활성화 함수는 학습을 위해서 필요한 존재들이다. 일단은 입력들의 계산 결과가 활성화 함수를 거치고 다음 뉴런으로
전달된다는 사실을 기억하자.
먼저 다양한 형태의 활성화 함수들을 살펴보자.
import numpy as np
def step_func(x):
y = x > 0
return y.astype(np.int)가장 단순한 형태의 함수인 계단함수를 구현하였다. 출력결과를 살펴보자.
>>> x = np.arange(-50, 50, 1)
>>> y = step_func(x)
>>> y
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])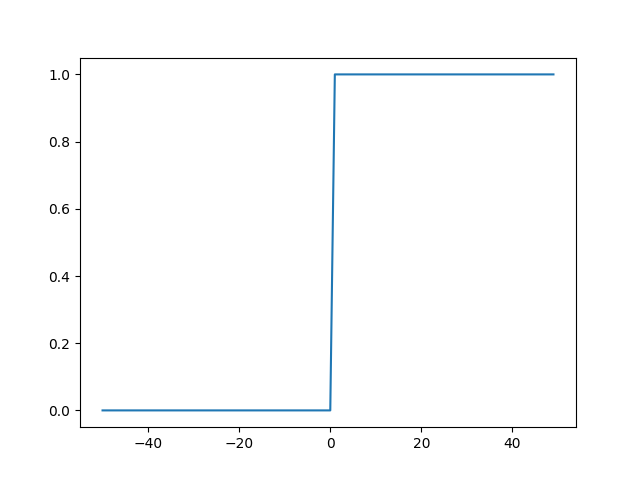
계단 함수를 x값이 0을 넘을때만 1을 출력하고 0 이하일 경우 0을 출력하도록 설계되어있다.
다음은 시그모이드 함수이다.

시그모이드 함수의 공식은 다음과 같다. 파이썬으로 구현해보자.
def sigmoid(x):
y = 1/(1+np.exp(-x))
return y결과를 살펴보자.
y = sigmoid(x)
>>> plt.plot(x,y)
>>> plt.show()
언뜻보면 계단함수와 생김새가 비슷하지만 가로축 0 인근에서 약간의 곡선 형태가 관찰된다.
이것이 계단함수와 구별되는 시그모이드 함수의 특징이다. 바로 '미분이 가능하다'는 것.
이렇게 활성화 함수에서 비선형 함수를 사용하는 이유는 무엇일까?
non-linear means that the output cannot be reproduced from a linear combination of the inputs (which is not the same as output that renders to a straight line--the word for this is affine).
another way to think of it: without a non-linear activation function in the network, a NN, no matter how many layers it had, would behave just like a single-layer perceptron, because summing these layers would give you just another linear function (see definition just above).
바로 활성화 함수가 비선형 함수라는 것은 출력이 입력들의 선형 결합으로부터 나오지 않았다는 것을 의미한다.
활성화 함수가 비선형 함수가 아니라면 아무리 층을 깊게 하더라도 단일층 퍼셉트론과 같은 효과를 낳는다.
이 비선형 함수들은 이후 신경망의 학습 과정에서 중요한 역할을 한다.
다음은 ReLU 함수이다.
def ReLU(x):
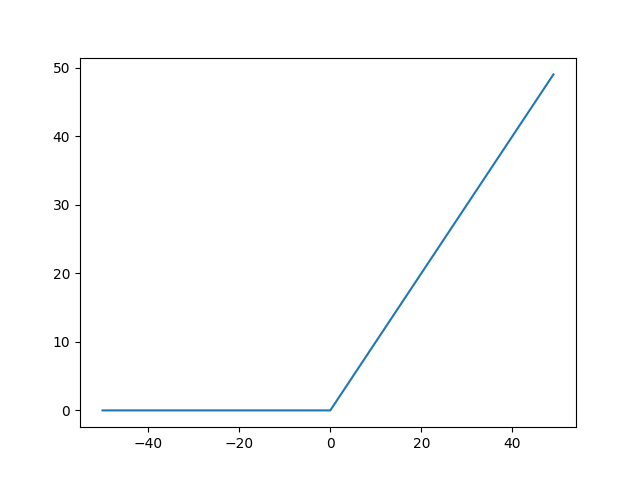
return np.maximum(0,x)ReLU 함수는 입력값이 0 이하면 0을 출력하고, 0을 넘어서면 x를 그대로 출력한다.
다시말하면 음수값들을 모두 무시해버린다.
지금까지 신경망의 정의와 활성화 함수에 대해서 간단히 알아보았다.
다음 장에서는 간단한 신경망을 구현하도록 하겠다.
'Deep Learning' 카테고리의 다른 글
| [밑바닥딥러닝] 6. 수치 미분, 편미분 (0) | 2021.10.01 |
|---|---|
| [밑바닥딥러닝] 5. 신경망 학습 - 손실 함수, 미니 배치 학습 (0) | 2021.09.30 |
| [밑바닥딥러닝] 4. 신경망 구현 - 손글씨 인식 (1) | 2021.09.12 |
| [밑바닥딥러닝] 3. 신경망 구현, 소프트맥스(softmax) (0) | 2021.09.12 |
| [밑바닥딥러닝] 1.퍼셉트론 (1) | 2021.09.10 |