2021. 10. 7. 20:24ㆍDeep Learning
본 게시글은 한빛미디어 『밑바닥부터 시작하는 딥러닝, 사이토 고키, 2020』의 내용을 참조하였음을 밝힙니다.
지난 장에서는 덧셈 노드와 곱셈 노드에서의 순전파와 역전파 방법에 대해서 살펴보았다.
이번 장에서는 저 두 노드 이 외에도 다양한 계산 노드의 순전파/역전파 구현을 알아보도록 하자.
활성화 함수 구현
1. ReLU 계층
첫번째로 알아볼 활성화 함수는 ReLU 함수이다.
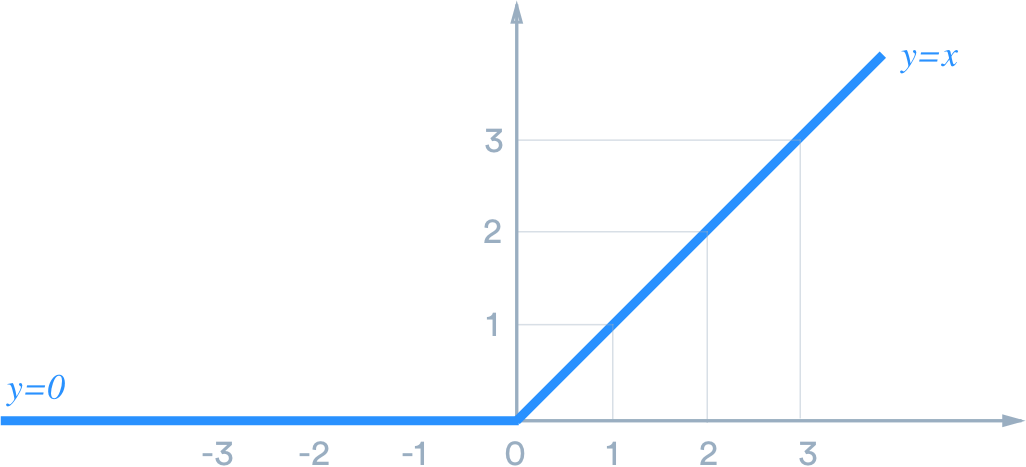
출처 : https://medium.com/@danqing/a-practical-guide-to-relu-b83ca804f1f7
ReLU 함수는 은닉층 노드에 적용되는 활성화 함수 중 하나로, 가중치 합(w1*x1 + w2*x2 + .... +b)이
0을 넘지 못한다면 해당 노드를 0으로 만들고, 0을 넘는다면 가중치 합 그대로를 출력하게끔 만드는
함수이다.

출처 : https://tex.stackexchange.com/questions/425073/vertical-spacing-for-table-with-equations
위는 활성화 함수 4가지와 그의 도함수(derivative)를 수식으로 나타낸 표이다.
ReLU 함수를 x에 대해서 미분하면 (x가) 0 이하 구간에서 0, 그리고 0 이상 구간에서 1을 반환한다.
ReLU 노드에 들어온 x는 곧 순전파 시 들어왔던 입력인 가중치 합이다.

위의 수식에서 순전파 시 입력이었던 부분은 Wx + b이다.
이 부분이 0 이하였을 경우에, 역전파가 흘려왔을 때 0을 곱하고, 0 이상이었을 경우에 역전파 그대로 보낸다.
이를 코드로 구현해보자.
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx인스턴스 변수인 mask는 순전파되었을 때의 값에 따라 (0을 기준으로) 결정되는 마스크 용도의 변수이다.
순전파를 수행하는 forward는 이전 은닉층 노드로부터 0 이하인 값만 뽑아내서 (이를 True로 규정) 해당되는
노드들에 대해서만 0으로 만들고 out을 반환한다.
mask 변수는 역전파 시에서도 동일한 마스크 변환을 수행해야 하기때문에 인스턴스 변수로 저장해둔다.
역전파인 backward에서는 흘러온 역전파 값에 (순전파 입력에 따라 결정된) mask를 적용하여 0으로 변환하여
반환한다.
2. Sigmoid 계층
다음으로 살펴볼 두번째 활성화 함수는 Sigmoid 함수이다.
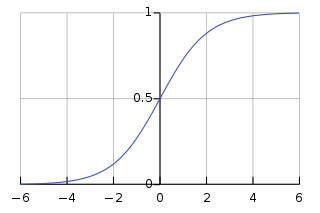
출처 : https://en.wikipedia.org/wiki/Sigmoid_function
Sigmoid 함수는 입력된 값(x)을 0과 1사이의 값으로 변환한다. 예측 모델이 이를 '확률'로서 해석할 수 있도록 한다.

출처 : https://tex.stackexchange.com/questions/425073/vertical-spacing-for-table-with-equations
위 표에 따라서 시그모이드 함수의 도함수는 (시그모이드가 반환하는 값이 y라고 한다면)
y*(1-y)가 된다.
시그모이드의 도함수를 구하는 자세한 과정은 아래를 참고하도록 하자.
Derivative of the Sigmoid function
In this article, we will see the complete derivation of the Sigmoid function as used in Artificial Intelligence Applications.
towardsdatascience.com
시그모이드를 코드로 구현해보자.
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = sigmoid(x)
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx순전파인 forward에서는 단순히 들어온 입력에 시그모이드 연산을 거쳐서 반환한다.
이 때 인스턴스 변수인 out에 순전파 시의 결과값을 저장해두는데, 이는 역전파 계산 때 이 결과값이 활용되기
때문이다. 역전파인 backward에서는 인스턴스 변수 out을 활용한 연산에 흘러온 역전파 값을 곱하여 반환해준다.
Affine/Softmax 계층 구현
대표적인 활성화 함수 구현을 알아보았으니 이번 절에서는 Affine 변환 계층과 Softmax 계층을 구현해보도록하자.
먼저 Affine 변환 계층부터 알아보자.
1. Affine 변환 계층
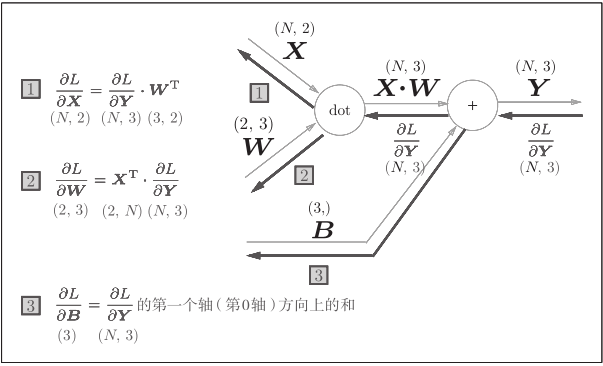
출처 : https://programmer.help/blogs/error-back-propagation-method.html
Affine 변환 계층의 순전파 과정은 다음과 같다.
1. 입력인 X 행렬과 가중치 행렬 W의 dot 연산을 한다. 여기서 출력 행렬의 크기는 (입력 크기, 은닉층 크기)
2. 편향 행렬인 b를 1 과정의 결과물에 더해준다. (편향 행렬의 크기는 (은닉층 크기))
역전파 과정에서는 덧셈 노드를 처음으로 만나 흘러온 역전파 값을 그대로 흘려보낸다.
다음으로 dot 곱셈 연산을 만나는데, 순전파 시의 곱셈 상대였던 행렬을 서로 바꿔서 역전파 값에 곱해준다.
이때 행렬 곱셈이 문제 없이 수행될 수 있도록 행렬 순서를 맞추거나, 전치행렬로 변환하여 형상을 바꾸어준다.
초기화 함수에서부터 차근차근 살펴보도록 하자.
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.original_x_shape = None
# 가중치와 편향 매개변수의 미분
self.dW = None
self.db = None
def forward(self, x):
...
def backward(self, dout):
...가중치 행렬인 W와 편향 행렬인 b를 파라미터로 받아 같은 이름의 인스턴스 변수에 저장한다.
순전파 시 입력인 x와 가중치에 대한 미분 dW, db 역시 인스턴스 변수로 저장해준다.
def forward(self, x):
# 텐서 대응
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return outforward 함수에서는 입력으로 들어온 x와 이의 shape를 인스턴스 변수에 저장해둔다.
그런 다음 넘파이의 dot 함수를 이용하여 행렬곱 연산을 수행하고 이를 반환한다.
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape) # 입력 데이터 모양 변경(텐서 대응)
return dxbackward 연산에서 x에 대한 미분은 흘러온 역전파 값에 순전파 시 가중치였던 W를 전치하여 행렬곱해준다.
가중치에 대한 미분(dW)은 반대로 순전파 시 입력인 x를 역전파 값에 행렬곱해준다.
편향인 b는 순전파시 각 배치 데이터마다 복제되어서 더해지기 때문에 역전파 때는 이를 반영하여
행렬의 배치 방향(axis = 0)으로 흘러온 역전파 행렬의 합(sum)을 계산해야한다.
backward 함수는 x에 대해서 미분한 값(dx)를 반환한다.
2. Softmax-with-loss
Softmax-with-loss 계층은 출력 노드들의 비율을 계산하는 Softmax 계층과 출력 노드에서 손실을 계산하는
Cross-Entropy-Error 계층을 연결한 계층이다.
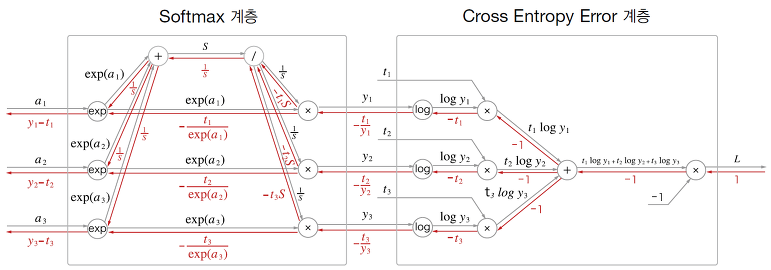
출처 : https://wjddyd66.github.io/dl/NeuralNetwork-(4)-Backpropagation2/
위 계층에서는 출력 노드들(a1, a2, a3)에 exponential 연산을 수행하고 이 exp(a)들의 합을 S로 한다.
각 exp(a)를 S로 나눈 값들이 y1, y2, y3이다. 이 값들이 Cross Entropy Error 계층에 진입하여 log 함수를
거치고 이들이 타깃값인 t1, t2, t3와 각각 곱해져서 하나의 덧셈노드에 모여서 총합이 연산된다.
최종적으로 -1를 곱해지면 최종 손실이 계산된다.
그림에서 순전파 밑에 빨간 글씨들이 역전파 값들인데, 최종적으로위 계층의 최종 역전파 값은 y-t 이다.
자세한 연산 과정은 아래를 참고하도록 하자.
Only Numpy: Implementing Mini VGG (VGG 7) and SoftMax Layer with Interactive Code
I wanted to practice my Back Propagation skills on Convolutional Neural Network. And I wanted to implement my own VGG net (from original…
towardsdatascience.com
Softmax-with-loss 계층을 코드로 구현해보자.
class SoftmaxWithLoss:
def __init__(self):
self.loss = None # 손실함수 출력
self.y = None # softmax의 출력
self.t = None # 정답 레이블(원-핫 인코딩 형태)
def forward(self, x, t):
....
def backward(self, dout=1):
....손실함수로 사용할 함수를 loss라는 인스턴스 변수에 저장하고, softmax의 출력인 y와 정답 레이블인 t도
객체에 저장한다.
class SoftmaxWithLoss:
def __init__(self):
....
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss순전파 forward에서는 타깃값 t와 입력값 x를 파라미터로 받아 x를 Softmax 함수를 통과시키고, 이를
Cross entropy error 함수에 (타깃값과 함께) 전달한다.
Cross entropy error에 따라 연산된 최종 손실을 반환한다.
class SoftmaxWithLoss:
def __init__(self):
....
def forward(self, x, t):
....
def backward(self, dout=1):
batch_size = self.t.shape[0]
if self.t.size == self.y.size: # 정답 레이블이 원-핫 인코딩 형태일 때
dx = (self.y - self.t) / batch_size
else:
dx = self.y.copy() # 원 핫 인코딩이 아니므로 y 형태를 복사
dx[np.arange(batch_size), self.t] -= 1 # t에 해당하는 인덱스를 1씩 빼준다(원 핫 인코딩이 아니므로!)
dx = dx / batch_size
# 순전파 시 loss 계산하면서 배치 전체에 대한 loss 총합으로 순전파 되기 때문에
# 역전파 시 배치크기로 나눠서 데이터 하나에 대한 역전파로 만든다.
return dx역전파 backward에서는 타깃값 t를 통해 배치 크기를 계산하고
t가 원 핫 인코딩되어있을 경우에 별다른 과정 없이 y-t를 배치 크기로 나눠서 반환한다.
원핫 인코딩이 아닐 경우 이를 처리하기 위한 과정을 수행한다.
dx를 배치 사이즈로 나눈 이유는 Cross entropy error 계산 시 배치 전체에 대한 loss를 계산하고 이를 배치 크기로
나눠 평균을 구하기 때문에 역전파 시에도 데이터 1개에 대한 역전파 값으로 만들기 위해서이다.
'Deep Learning' 카테고리의 다른 글
| [밑바닥딥러닝] 12. 매개변수 갱신법 (1) | 2021.10.16 |
|---|---|
| [밑바닥딥러닝] 11. 오차역전파법(backpropagation) 구현(2) (1) | 2021.10.07 |
| [밑바닥딥러닝] 9. 오차역전파법(backpropagation) - 계산그래프 (1) | 2021.10.03 |
| [밑바닥딥러닝] 8. 2층 신경망 구현, 미니배치 학습 (0) | 2021.10.01 |
| [밑바닥딥러닝] 7. 경사하강법(gradient descent) (0) | 2021.10.01 |