2021. 10. 7. 20:48ㆍDeep Learning
본 게시글은 한빛미디어 『밑바닥부터 시작하는 딥러닝, 사이토 고키, 2020』의 내용을 참조하였음을 밝힙니다.
8장에서 살펴보았던 2층 신경망 구현에서는 가중치에 대한 편미분을 수행해 이를 가중치 갱신에 반영하였다.
https://humankind.tistory.com/57
[밑바닥딥러닝] 8. 2층 신경망 구현, 미니배치 학습
본 게시글은 한빛미디어 『밑바닥부터 시작하는 딥러닝, 사이토 고키, 2020』의 내용을 참조하였음을 밝힙니다. 이번 장에서는 지금까지 살펴본 신경망의 출력, 손실 함수, 그레디언트, 가중치
humankind.tistory.com
하지만 이는 시간 복잡도 측면에서 매우 비효율적인 방법이었고, 오차역전파법이 그 대안이 될 수 있다는 사실을
확인하도록 하자!
2층 신경망 구현
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.lastlayer = SoftmaxWithLoss()가중치 갱신하는 방법은 이전과 다를 바가 없다.
가중치와 입력을 다루는 계층들(Affine, Relu)을 layers라는 변수에 모아서 저장한다.
마지막 출력층은 SoftmaxwithLoss 계층을 지나도록한다.
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
return self.lastlayer.forward(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
# score로 표현된 y값에서 가장 대표(큰) 값의 인덱스를 뽑아냄.
if t.ndim != 1 : t = np.argmax(t, axis=1)
# 타깃이 한 데이터만 갖는게 아니라면, t에도 마찬가지로 대표값 뽑는다.
accuracy = np.sum(y == t)/float(x.shape[0])
# y와 t가 일치하는 횟수를 count하고 배치 수로 나눠 평균 get
return accuracypredict 함수에서는 layers에 저장된 모든 계층들을 지난 최종 출력을 반환하도록 하고,
손실을 계산하는 loss 함수에서는 예측된(predict) 값을 바탕으로 마지막 출력층(Softmaxwithloss)을 통과시켜
최종 손실을 반환한다. loss 함수에서는 모든 계층(layers + last layer)을 통과(forward)시킨다.
정확도를 계산하는 accuracy 함수에서는 score로 표현된 y값에서 가장 큰 인덱스를 추출하여 이를 t값과 비교하여
정답인 비율을 계산하여 반환한다.
def gradient(self, x, t):
self.loss(x, t)
dout = 1
dout = self.lastlayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
grads = {}
grads['W1'] = self.layers['Affine1'].dW
grads['b1'] = self.layers['Affine1'].db
grads['W2'] = self.layers['Affine2'].dW
grads['b2'] = self.layers['Affine2'].db
return grads그레디언트를 구하는 gradient 함수에서는 loss 함수를 호출하여 모든 계층을 통과하도록 한다.
그다음 가장 최종 층(lastlayer)부터 backward 함수를 순차적으로 호출하여 역전파값들을 구한다.
각 가중치(W1, b1, W2, b2)에 대한 그레디언트들은 각 계층 객체에 저장된 인스턴스 변수를 가져와서
이를 grads라는 변수에 딕셔너리 형태로 저장하고 이를 반환한다.
학습 수행
predictor = TwoLayerNet(784, 50, 10)
(x_train, t_train), (x_test, t_test) = \
load_mnist(normalize=True, one_hot_label=True)
iternum = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1가중치들의 크기를 초기화하기 위한 파라미터들로 최초 입력층의 크기는 784, 은닉층의 크기는 50, 출력층 크기는
10으로 설정하였다.
반복 횟수는 10000번, 훈련 크기와 배치 크기를 지정하고, 학습률은 0.1로 설정해준다.
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size/batch_size, 1)과대 적합 여부를 알아보기 위한 리스트 변수들과 에포크 반복횟수 변수를 선언해준다.
for i in range(iternum):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
grads = predictor.gradient(x_batch, t_batch)
for key in ('W1', 'b1', 'W2', 'b2'):
predictor.params[key] -= 0.01*grads[key]
loss = predictor.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i%iter_per_epoch == 0:
train_acc = predictor.accuracy(x_train, t_train)
test_acc = predictor.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print(train_acc, test_acc)각 반복(iter)마다 배치를 무작위로 선정하고, 예측 모델에서 그레디언트를 계산하고 각 가중치마다 이를 반영하여
갱신한다.
훈련세트에서의 손실값과 에포크마다의 훈련세트/테스트세트에서의 정확도 비교를 해보자.
plt.plot(train_acc_list, 'b-', label = 'train accuracy')
plt.plot(test_acc_list, 'g--', label = 'test accuracy')
plt.title('accuracy in train VS accuracy in test')
plt.xlabel('iter')
plt.ylabel('accuracy')
plt.legend(loc='best')
plt.grid(linestyle='dotted')
plt.show()
plt.plot(train_loss_list, label='loss')
plt.title("predictor's losses in train data")
plt.xlabel('iter')
plt.ylabel('loss')
plt.legend(loc='best')
plt.grid(linestyle='dotted')
plt.show()
손실이 요동치긴하지만 반복을 거듭함에 따라 손실이 점차 낮아지는 것을 확인할 수 있다.
그래프가 요동치는 것은 가중치 갱신이 '항상' 올바른 방향으로만 이루어진다는 것은 아니라는 사실을
의미한다. 다만 거시적 관점으로는 손실을 줄이는 쪽으로 갱신된다.
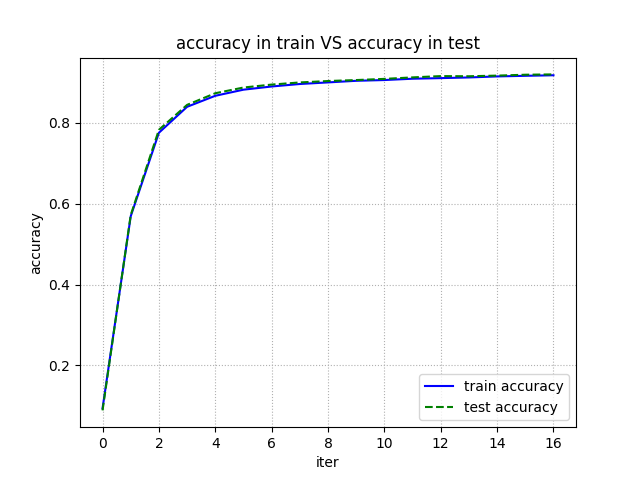
훈련 세트 내에서만의 데이터를 통해 가중치 갱신을 했음에도 테스트 세트에서의 예측이
훈련 세트에서의 예측과 크게 다르지 않다. 이는 예측 모델이 과대적합(overfitting)되지 않았음을
의미한다.
'Deep Learning' 카테고리의 다른 글
| [밑바닥딥러닝] 13. 모델 가중치의 초기화 (0) | 2021.10.16 |
|---|---|
| [밑바닥딥러닝] 12. 매개변수 갱신법 (0) | 2021.10.16 |
| [밑바닥딥러닝] 10. 오차역전파법(backpropagation) 구현(1) (0) | 2021.10.07 |
| [밑바닥딥러닝] 9. 오차역전파법(backpropagation) - 계산그래프 (0) | 2021.10.03 |
| [밑바닥딥러닝] 8. 2층 신경망 구현, 미니배치 학습 (0) | 2021.10.01 |