2023. 2. 25. 02:11ㆍNatural Language Processing
지난 장에서는 RNN이 무엇인지 살펴보고, RNN을 통해서 어떻게 모델이
장기 기억을 가져가는지 알아보았다. 하지만 RNN은 Time이 늘어짐에 따라
역전파 과정에서 기울기 소실/폭발이 일어날 수 있다는 문제점이 있다.
이번 장에서는 이러한 문제점을 극복할 수 있는 LSTM을 알아보고 구현하도록 해보자.
LSTM은 Long Short-Term Memory의 약자로 '기억 셀'이라는 요소를 통해서 시계열에서
어떤 지점을 기억하고, 잊을지에 대해서도 학습하는 더 발전된 형태의 순환신경망이다.
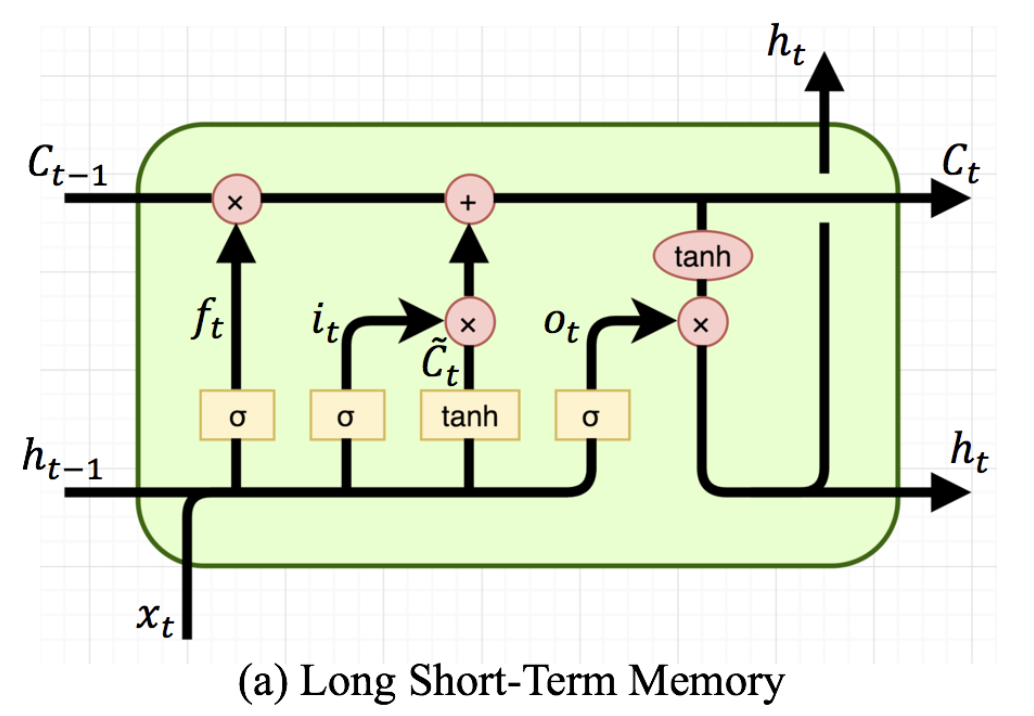
기존 RNN에서는 이전 타임(t-1)에서 은닉 상태(h_t-1)를 전달받아서 현재(t)의 은닉 상태(h_t)를 계산해냈다.
LSTM에서는 이 중간 계산 과정에 여러가지 게이트들(f, g, i, o)을 추가해서 어떤 시점(t)의 입력(x)을 얼마나 기억해야할지
얼마나 잊어야할지를 학습할 수 있다.
LSTM은 기억 셀(c)을 유지하는데, 은닉상태(h)와는 다르게 이 LSTM을 다음 시점의 LSTM에만 보내준다.
다음 LSTM에서는 전달받은 은닉상태(h_t-1)와 기억셀(c_t-1)의 정보를 가지고 새로운 은닉 상태와 기억 셀을 계산해낸다.
import numpy as np
from common.functions import sigmoid
class LSTM:
def __init__(self, Wx, Wh, b):
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.cache = None가장 단순한 LSTM을 구현해보자. 위 클래스는 한 입력(ex) cat)을 처리해서 은닉 상태(h)와 기억 셀(c)을 생성해낸다.
def forward(self, x, h_prev, c_prev):
Wx, Wh, b = self.params
#4개 게이트의 가중치가 다 담겨있음
N, H = h_prev.shape
A = np.matmul(x, Wx) + np.matmul(h_prev, Wh) + b
f = A[:, :H]
g = A[:, H:2*H]
i = A[:, 2*H:3*H]
o = A[:, 3*H:]
f = sigmoid(f)
g = np.tanh(g)
i = sigmoid(i)
o = sigmoid(o)
c_next = f * c_prev + g * i
h_next = o * np.tanh(c_next)
self.cache = (x, h_prev, c_prev, i, f, g, o, c_next)
return h_next, c_next각 게이트들(f, g, i, o)들은 각자의 가중치(Wx, Wh, b)를 유지하고 있으며 학습 시 가중치들이 갱신된다.
f (forget)게이트는 이전 기억 셀(c_prev)의 정보를 얼마나 유지할 것인지는 정하고,
g 게이트는 현재 시점의 새로운 입력을 기억하기 위해서 존재하고, 이 기억을 '얼마나' 기억할 것인지는
i (input) 게이트가 정한다. 시그모이드 함수는 데이터를 0~1 사이의 값으로 만들어주는데 이 함수가 게이트에 사용되면
정보 유지 정도를 정하는데 사용될 수 있다.
마지막으로 o (output) 게이트는 계산된 기억 셀(c) 정보를 다음 은닉 상태에 얼마나 반영할 것인지는 정한다.
import numpy as np
from LSTM import LSTM
class TimeLSTM:
def __init__(self, Wx, Wh, b, stateful = False):
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.layers = None
self.h, self.c = None, None
self.dh = None
self.stateful = stateful시계열 정보(xs)가 들어오면 한번에 처리할 수 있도록 LSTM을 묶어서 TimeLSTM 계층을 구현하였다.
def forward(self, xs):
Wx, Wh, b = self.params
N, T, D = xs.shape
H = Wh.shape[0]
self.layers = []
hs = np.empty((N, T, H), dtype='f')
#생성할 hs 틀 만듦
if not self.stateful or self.h is None:
self.h = np.zeros((N, H), dtype='f')
#stateful 하지 않으면 이어받을 은닉상태 h 없으므로 새로 생성
if not self.stateful or self.c is None:
self.c = np.zeros((N, H), dtype='f')
# stateful 하지 않으면 이어받을 기억셀 c 없으므로 새로 생성
for t in range(T):
layer = LSTM(*self.params)
self.h, self.c = layer.forward(xs[:, t, :], self.h, self.c)
#한 time의 LSTM forward하고 h, c 갱신
hs[:, t, :] = self.h
self.layers.append(layer)
#시점 t에서의 LSTM 이어붙임
return hs순전파 과정은 시계열 크기(T)에 따라 LSTM 계층에 입력(x)을 하나하나 통과시키고 새로운 h, c를 계산한다.
이를 다음 LSTM 계층에 전달한다. 최종적으로 TimeLSTM 계층이 계산하는 은닉상태들(hs)을 반환한다.
def backward(self, dhs):
Wx, Wh, b = self.params
N, T, H = dhs.shape
D = Wx.shape[0]
dxs = np.empty((N, T, D), dtype='f')
#역전파할 dxs 틀 생성
dh, dc = 0, 0
grads = [0, 0, 0]
for t in reversed(range(T)):
#시간 거꾸로 내려오면서
layer = self.layers[t]
dx, dh, dc = layer.backward(dhs[:, t, :]+dh, dc)
#나중 시점의 LSTM부터 역전파
dxs[:, t, :] = dx
for i, grad in enumerate(grads):
grads[i] += grad
#Wx, Wh, b별로 gradient값 누적
for i, grad in enumerate(grads):
self.grads[i][...] = grad
self.dh = dh
#가장 마지막으로 전파된 dh를 저장
return dxs역전파 과정은 시계열의 마지막 시점부터 시작해서 역전파 값(dh, dc)들을 이전 시점의 LSTM으로 흘려보낸다.
최종적으로 입력에 대한 그레디언트인 dxs를 반환한다.
class Rnnlm:
def __init__(self, vocab_size=10000, wordvec_size=100, hidden_size=100):
V, D, H = vocab_size, wordvec_size, hidden_size
rn = np.random.randn
embed_W = (rn(V, D) / 100).astype('f')
lstm_Wx = (rn(D, 4 * H) / np.sqrt(D)).astype('f')
lstm_Wh = (rn(H, 4 * H) / np.sqrt(H)).astype('f')
lstm_b = np.zeros(4 * H).astype('f')
affine_W = (rn(H, V) / np.sqrt(H)).astype('f')
affine_b = np.zeros(V).astype('f')
#가중치 생성
self.layers = [
TimeEmbedding(embed_W),
TimeLSTM(lstm_Wx, lstm_Wh, lstm_b),
TimeAffine(affine_W, affine_b)
]
self.loss_layer = TimeSoftmaxWithLoss()
self.lstm_layer = self.layers[1]
self.params, self.grads = [], []
for layer in self.layers:
self.params += layer.params
self.grads += layer.gradsLSTM이 은닉 상태와 기억 셀 계산한 이후에는 이 응축된 데이터를 '단어(실제론 임베딩된)' 로 바꿔주어야 한다.
먼저 입력 데이터 I / am / a / cat 가 들어오면 이를 임베딩하여 0 / 1 / 2 / 3 으로 형태를 바꿔준 뒤에
임베딩 데이터를 LSTM 계층에 통과시켜 시계열 은닉상태(hs)를 얻는다.
이 hs를 어파인 변환 시켜서 단어 사전 크기만큼 바꿔서 예측 단어 후보를 선정할 수 있도록 한다.
이를 위해 소프트맥스 계층과 크로스 엔트로피 손실 계층을 하나로 합친 계층을 마지막에 둔다.
def predict(self, xs):
for layer in self.layers:
xs = layer.forward(xs)
score = xs
return score순전파 과정은 다음과 같다.
입력 데이터를 임베딩, LSTM, 어파인변환 계층에 통과시켜서 score 값을 구한다.
def forward(self, xs, ts):
score = self.predict(xs)
#입력된 xs에 대한 결과를 반환한다.
loss = self.loss_layer.forward(score, ts)
#score 데이터를(softmax 후) target 데이터와 비교하여 loss 계산
return loss그 뒤에 이 score 값을 softmax 계층에 통과시켜서 확률화하고 크로스엔트로피 손실까지 계산하여 이를 반환한다.
def backward(self, dout=1):
dout = self.loss_layer.backward(dout)
for layer in reversed(self.layers):
dout = layer.backward(dout)
return dout역전파 과정은 소프트맥스 계층부터 차례로 역전파한다.
# coding: utf-8
import sys
sys.path.append('..')
from common.optimizer import SGD
from common.trainer import RnnlmTrainer
from common.util import eval_perplexity
from dataset import ptb
from Rnnlm import Rnnlm
# 하이퍼파라미터 설정
batch_size = 20
wordvec_size = 100
hidden_size = 100 # RNN의 은닉 상태 벡터의 원소 수
time_size = 35 # RNN을 펼치는 크기
lr = 20.0
max_epoch = 1
max_grad = 0.25
# 학습 데이터 읽기
corpus, word_to_id, id_to_word = ptb.load_data('train')
corpus_test, _, _ = ptb.load_data('test')
vocab_size = len(word_to_id)
xs = corpus[:-1]
ts = corpus[1:]
# 모델 생성
model = Rnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)
trainer = RnnlmTrainer(model, optimizer)
# 기울기 클리핑을 적용하여 학습
trainer.fit(xs, ts, max_epoch, batch_size, time_size, max_grad,
eval_interval=20)
trainer.plot(ylim=(0, 500))
# 테스트 데이터로 평가
model.reset_state()
ppl_test = eval_perplexity(model, corpus_test)
print('테스트 퍼플렉서티: ', ppl_test)epoch를 1로 설정하였을 때 모델에 대한 퍼플렉시티 평가는 아래와 같이 나타난다.

epoch를 1회 돌렸을 때 퍼플렉시티는 200~300 사이의 값을 보인다.
실제로 epoch 수를 늘렸을 때 퍼플렉시티 값이 더 내려갈 것이다.
'Natural Language Processing' 카테고리의 다른 글
| [NLP] Attention (0) | 2023.02.26 |
|---|---|
| [NLP] Seq2seq (0) | 2023.02.26 |
| [NLP] RNN(순환 신경망) (0) | 2023.02.22 |
| [NLP] word2vec 개선 - 임베딩, 네거티브 샘플링 (0) | 2023.02.19 |
| [NLP] word2vec (0) | 2023.02.13 |